Question 929310: 1. You have deposited $7,000 in an account that pays 6.25% interest compounded continuously. How long will it take your money to double?
2. You have deposited $12,000 in an account compounded monthly. After 7 years the balance has grown to $15,532. Find the rate.
PLEASE HELP ME ANSWER THESE 2 QUESTIONS!!!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. For continuous compounding, the balance amount  is related to is related to
the principal (initial investment  , ,
the rate  (written as a decimal), and (written as a decimal), and
the time in years,  , by the formula , by the formula
 . .
The number  is an irrational number like is an irrational number like  that come up pretty often . It is not invented to make students learn one more number; it just comes up naturally. that come up pretty often . It is not invented to make students learn one more number; it just comes up naturally.
We use it as a base for powers, and of course for logarithms that we call natural logarithms

So, for  , ,  , and , and  , we can write , we can write
 ---> ---> 
Note that we did not need to know the amount invested.
 ---> --->  (taking natural logarithms on both sides). (taking natural logarithms on both sides).
Using the approximate value  , ,
 --> --> --> --> (rounded). (rounded).
So, it will take 11 years for the money to double.
2. $12,000 compounded monthly. After 7 years the balance has grown to $15,532. Find the rate.
For monthly compounding, the balance grow by 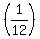 of the yearly rate every month. of the yearly rate every month.
So over  , the balance grew by a factor of , the balance grew by a factor of  applied applied  times to times to
 . .
Solving for rate:





Using logarithm base 10 for an approximate calculation:


Reversing the logarithm by calculating power of 10 on both sides of the equal sign:





|
|
|