|
Question 928247: Bob wants to cut a wire that is 60 cm long into two pieces. Then he wants to make each piece into a square. Determine how the wire should be cut so that the total area of the two squares is as small as possible.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  be the length of one of the pieces, in cm. be the length of one of the pieces, in cm.
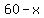 = the length of the other piece, in cm. = the length of the other piece, in cm.
The sides of the squares made will measure  and and  cm, cm,
and the areas of those squares, in square cm, will be
 and and  respectively. respectively.
The total area of ththe two squares, in square cm, will be

That expression, like  is a quadratic function of is a quadratic function of  . .
Quadratic functions have the general form  , ,
and if  the quadratic function has a minimum at the quadratic function has a minimum at  . .
Both, 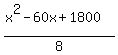 and and  , have a minimum at , have a minimum at
 --> --> . .
So, to make the total area of the two squares is as small as possible, the wire should be cut in half, making two 30-cm pieces.
|
|
|
| |