Question 928231: find equation of hyperbola where foci is (9,0) and hyperbola passes through (12,3)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! find equation of hyperbola where foci is ( , , ) and hyperbola passes through ( ) and hyperbola passes through ( , , ) )
The general formula of a hyperbola is:

Since, ( , ,  ) is a point on the hyperbola, we have: ) is a point on the hyperbola, we have:

 ........eq.(1) ........eq.(1)
Since the foci is ( , , ), we have: ), we have:

 .....eq.(2) .....eq.(2)
Substituting (2) into (1), we have:
 ....common denominator is ....common denominator is 





 ....write ....write 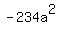 as as 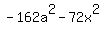




solutions:
=> => =>
=> => =>
Suppose  , from (2), we have: , from (2), we have:
 =>rejected, since a square cannot be negative =>rejected, since a square cannot be negative
Suppose  , from (2), we have: , from (2), we have:
 => this solution is accepted => this solution is accepted
Thus, we have:

foci is ( , , ) and ( ) and ( , , ) )
hyperbola passes through ( , , ) )

|
|
|