Question 928146: How can I create a "roller coaster" ( polynomial function) with:
3 relative maximums or minimums
The first maximum at 250 ft
A length of 4 minutes
A tunnel beneath the ground(x axis)
An additional tunnel or relative maximum or minimum
I'm really confused
Found 2 solutions by stanbon, KMST:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! How can I create a "roller coaster" ( polynomial function) with:
3 relative maximums or minimums
The first maximum at 250 ft (not sure if that means x=250 or y = 250)
A length of 4 minutes
A tunnel beneath the ground(x axis)
An additional tunnel or relative maximum or minimum
----
Before you try the math you should sketch the path of the coaster.
---------
It starts at ground level, rises relative max at 250 ft, falls to a relative min
at ?, rises to relative max ??, then falls to ground level at time = 4 minutes.
----------------
The function must be 4th degree.
Its derivative is a cubic with 3 Real zeros
-----
The 4 minutes can be the last zero of the function.
----
Cheers,
Stan H.
=================
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! It is confusing.
I assume the expected polynomial answer represents height in feet (y) as a function of time in minutes (x).
The domain of the function would be  , the span of time from beginning to end of the ride. , the span of time from beginning to end of the ride.
It does not matter if the "shadow" of the ride on the ground is a straight line or curves to let the riders exit near the entrance to the ride.
They do not require that it obeys the laws of physics, either.
Without using calculus, I would recommend using a graphing calculator or a spreadsheet program, such as Excel.
A polynomial would have at most as many maxima and minima as its grade minus 1.
In other words, to have "3 relative maximums or minimums" the grade of the polynomial must be at least 4,
and to have an additional maximum or minimum, the grade of the polynomial must be at least 5.
The sign (positive or negative) of the  height value is easy to see when the polynomial is in factored form. height value is easy to see when the polynomial is in factored form.
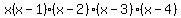 is a degree 5 polynomial with zeros at is a degree 5 polynomial with zeros at
 , ,  , ,  , ,  , and , and  . .
(That would make equal to zero the value of the polynomial - the height of the ride - at  and and  , so the beginning and end of the ride would be at ground level. That makes it halfway realistic). , so the beginning and end of the ride would be at ground level. That makes it halfway realistic).
That polynomial changes sign at each zero.
It is obviously positive for  , where all factors would be positive, , where all factors would be positive,
so it must be positive for 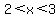 and and  , ,
and it must be negative for 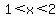 and and 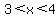 (two tunnels). (two tunnels).
In between zeros, it must hit maxima at some point in 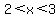 and and  , ,
and it must reach minima at some point in 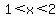 and and 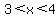 . .
That gives you 2 maxima and 2 minima.
You can graph the function with a graphing calculator or a computer plus some software. Because the 5 zeros are evenly spaced by design, it is symmetrical around point (2,0).
 Not realistic looking, but may get credit. Not realistic looking, but may get credit.
You can find the approximate  and and  values for the first maximum with a graphing calculator, or some other software. (It would take a lot of trial and error calculations otherwise). A good approximation for values for the first maximum with a graphing calculator, or some other software. (It would take a lot of trial and error calculations otherwise). A good approximation for  is is  , which makes the value of the polynomial , which makes the value of the polynomial  . .
You could make that first relative maximum 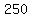 by just applying an ugly factor: by just applying an ugly factor:
 has the same shape, but the first maximum is at a height of 250 feet. has the same shape, but the first maximum is at a height of 250 feet.
With a graphing calculator you may be able to plat with the spacing between the zeros, to get a graph you like better. If you want to reach a higher maximum in between two zeros, space those zeros a little farther apart.
If you want the graph to be horizontal at some zero, make it a double zero. For example if you want the track to be level at zero height at the end of the ride, include  as a factor so as a factor so  will be a zero and a maximum or minimum. will be a zero and a maximum or minimum.
Your ride can start on uphill track, or downhill track, as for  , with one zero at , with one zero at  . .
That function would also let your riders get off on level tracks (because of the  factor), and would look like this: factor), and would look like this:
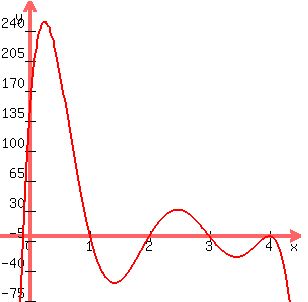 In this case, the first maximum is a relative maximum. In this case, the first maximum is a relative maximum.
For an almost level start, you could try changing the spacing of the zeros on either side of  , ,
as in the polynomials 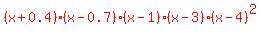 , or , or 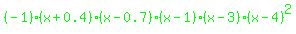
 . .
If you were to choose 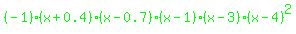 , ,
it has a first absolute maximum at  where the value of the polynomial is where the value of the polynomial is 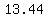 , and a first relative maximum at about , and a first relative maximum at about  , where the value of the polynomial is , where the value of the polynomial is 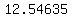 (rounded). The question then is do we make the height reach 250 feet at the first (absolute) maximum at (rounded). The question then is do we make the height reach 250 feet at the first (absolute) maximum at  by using by using
 , ,
or should it reach 250 feet at the first relative maximum at  , ,
and then the function would be  . .
|
|
|