SOLUTION: Verify the quadrilateral formed by joining midpoint of sides of a quadrilateral is a parallelogram's

Algebra ->  Geometry-proofs -> SOLUTION: Verify the quadrilateral formed by joining midpoint of sides of a quadrilateral is a parallelogram's      Log On


   

Question 928077: Verify the quadrilateral formed by joining midpoint of sides of a quadrilateral is a parallelogram's
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I assume that what is expected is an analytical geometry proof.
Let the quadrilateral be OABC, and let the vertices and their coordinates be
O%280%2C0%29 ,
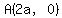A%282a%2C0%29 ,
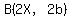B%282X%2C2b%29 , and
C%282c%2C2Y%29 .
Those assumptions pose no restrictions, because
I can call the vertices any letter I chose;
I can always place my system of coordinates with one vertex is at the origin, and another vertex on the x-axis, and
all coordinates could be divided by 2 to make my a , b , c, X , and Y .

The midpoint of OA is 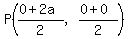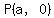P%28%280%2B2a%29%2F2%2C%280%2B0%29%2F2%29 ---> P%28a%2C0%29 .
The midpoint of AB is 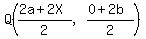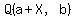Q%28%282a%2B2X%29%2F2%2C%280%2B2b%29%2F2%29 ---> Q%28a%2BX%2Cb%29 .
The midpoint of BC is 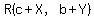R%28%282c%2B2X%29%2F2%2C%282Y%2B2b%29%2F2%29 ---> R%28c%2BX%2Cb%2BY%29 .
The midpoint of OC is 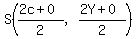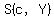S%28%282c%2B0%29%2F2%2C%282Y%2B0%29%2F2%29 ---> S%28c%2CY%29 .

PQRS is a parallelogram if PQ is parallel to RS and PS is parallel to QR.
The slope of PQ is %28b-0%29%2F%28a%2BX-a%29=b%2FX ,
and the slope of RS is %28b%2BY-Y%29%2F%28c%2BX-c%29=b%2FX ,
so PQ and RS are parallel.
The slope of PS is %28Y-0%29%2F%28c-a%29=Y%2F%28c-a%29 ,
and the slope of QR is %28b%2BY-b%29%2F%28c%2BX-%28a%2BX%29%29=Y%2F%28c%2BX-X-a%29=Y%2F%28c-a%29 ,
so PS and QR are parallel.
Since PQ is parallel to RS and PS is parallel to QR, PQRS is a parallelogram.