Question 928076: In an arithmetic series, t10=21 and t19=48
Find a, d, and S23
Thank You
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I assume  = first term, = first term, 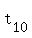 = tenth term, = tenth term, 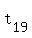 = term number = term number  , and , and 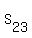 = sum of first = sum of first 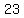 terms. terms.
It is commonly understood that  = common difference. = common difference.
 , so , so
 ---> ---> ---> ---> ---> ---> ---> --->
Then,  ---> ---> ---> ---> ---> ---> ---> ---> . .
There are different formulas to calculate sums of arithmetic sequences, but I prefer to remember that adding up the first  terms twice, grouping them in pairs "head-to-tail", terms twice, grouping them in pairs "head-to-tail", 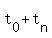 , , 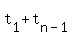 , , 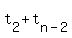 , and so on, you end up with a sum of , and so on, you end up with a sum of  pairs that all add up to pairs that all add up to 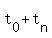 , so , so
 --> --> . .
So,  and and  . .
|
|
|