|
Question 927902: 4x^2-3y^2+16x+2y=25/3
Identify if it is a hyperbola, parabola, or ellipse and label the center point, vertex points, focus points, asymptote equations, a length, b length, and c length, and the transverse axis.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 The equation is
The equation is      The center is
The center is 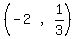 The vertices are the points
The vertices are the points 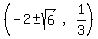 The foci are the points
The foci are the points 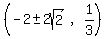 The equations of the asymbtotes in point slope form are
The equations of the asymbtotes in point slope form are
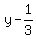 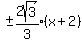 How'd I get all that?
1. I knew it was a hyperbola because the x² and y² terms in
How'd I get all that?
1. I knew it was a hyperbola because the x² and y² terms in
 have coefficients of opposite
signs when on the same side of the equation. But I didn't
know whether it was going to be a hyperbola
like this: have coefficients of opposite
signs when on the same side of the equation. But I didn't
know whether it was going to be a hyperbola
like this:  or like this: or like this:  So I started with
So I started with
  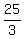 Get the term next to the x² term and the y term next
to the y² term
Get the term next to the x² term and the y term next
to the y² term
  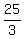 On the left, factor out 4 out of the first two terms
and -3 out of the last two terms. The unusual part
is having to factor -3 out of a +2y, for you never had
to do such a thing in basic algebra. Just remembr that
"to factor out" means "to divide by", so you divide +2y
by -3 and you get
On the left, factor out 4 out of the first two terms
and -3 out of the last two terms. The unusual part
is having to factor -3 out of a +2y, for you never had
to do such a thing in basic algebra. Just remembr that
"to factor out" means "to divide by", so you divide +2y
by -3 and you get  : :
  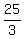 Then inside those parentheses you must complete the square:
In the first parentheses:
1. Multiply the coefficient of the x term, which is +4, by
Then inside those parentheses you must complete the square:
In the first parentheses:
1. Multiply the coefficient of the x term, which is +4, by  ,
getting +2.
2. Square +2 getting +4.
3. Put +4-4 after the x term. (That is, add it and subtract 4, which
amounts to adding 0) ,
getting +2.
2. Square +2 getting +4.
3. Put +4-4 after the x term. (That is, add it and subtract 4, which
amounts to adding 0)
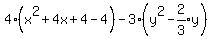  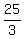 In the second parentheses:
1. Multiply the coefficient of the y term, which is
In the second parentheses:
1. Multiply the coefficient of the y term, which is  , by , by  ,
getting ,
getting  .
2. Square .
2. Square  getting getting  .
3. Put .
3. Put 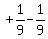 after the y term. (That is, add it and subtract after the y term. (That is, add it and subtract  , which
amounts to adding 0) , which
amounts to adding 0)
  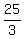 Group the first three terms in each parentheses:
Group the first three terms in each parentheses:
  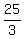 Factor
Factor  as as  and then as and then as  Factor
Factor  as as  and then as and then as 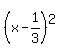 and so we have:
and so we have:
  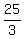 Now we have to remove the BIG parentheses by distributing
without disturbing the smaller parentheses, like this:
Now we have to remove the BIG parentheses by distributing
without disturbing the smaller parentheses, like this:
  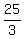 Subtract the
Subtract the  from both sides since that will make a whole
number on the right: from both sides since that will make a whole
number on the right:
  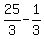
  
  
   Now we get 1 on the right by dividing through by 24
Now we get 1 on the right by dividing through by 24
  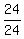
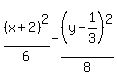   Now that's in the form of a hyperbola like this
Now that's in the form of a hyperbola like this  . .
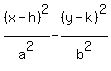  
 , ,  , ,  , ,  So we have the center.
The foci ar points which are "a" units right and left of the center.
The defining rectangle is 2a units wide and 2b units high.
It's extended diagonals are the asymptotes.
To find the foci we calculate c from c² = a²+b², and they are c
units right and left of the center.
The asymptotes have slopes
So we have the center.
The foci ar points which are "a" units right and left of the center.
The defining rectangle is 2a units wide and 2b units high.
It's extended diagonals are the asymptotes.
To find the foci we calculate c from c² = a²+b², and they are c
units right and left of the center.
The asymptotes have slopes 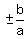 and pass through the
center, so you can find them from the point-slope form.
Edwin and pass through the
center, so you can find them from the point-slope form.
Edwin
|
|
|
| |