Question 927825: A CLUB HAS 30 FRESHMEN, 25 SOPHOMORES, 40 JUNIORS. 6 ARE CHOSEN AT RANDOM, WHATS THE PROBABILITY THAT 2 OF EACH ARE CHOSEN.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!  club members.
From all the club members,
 different groups of 6 can be made.
How many of those groups include 2 freshmen, 2 sophomores and 2 juniors?
How many different groups of 6 can be made, including 2 freshmen, 2 sophomores and 2 juniors?
There are 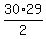 ways to choose a group of 2 freshmen out of the 30 freshmen in the club.
There are  ways to choose a group of 2 sophomores out of the 25 sophomores in the club.
There are  ways to choose a group of 2 juniors out of the 40 juniors in the club.
So, there are 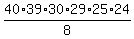 different groups of 6 than can be made, including 2 freshmen, 2 sophomores and 2 juniors.
As a fraction of all the groups of 6 that can be made, that is
 ,
and, as any group is as likely as any other group,
that is the probability that the randomly chosen group of 6 will contain exactly 2 students from each class.
 (rounded)
You could say that the probability of such a group is 11.7%.
|
|
|
