SOLUTION: The slope of the line segment is 3 and one endpoint is (-2,5). If the other endpoint is on the axis, what are the coordinates?

Algebra ->  College  -> Linear Algebra -> SOLUTION: The slope of the line segment is 3 and one endpoint is (-2,5). If the other endpoint is on the axis, what are the coordinates?      Log On


   

Question 927703: The slope of the line segment is 3 and one endpoint is (-2,5). If the other endpoint is on the axis, what are the coordinates?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
On what axis? The x-axis? The y-axis? Never mind; we can find both.

Using the data given, a point-slope form of the equation of the line can be written as
y-5=3%28x-%28-2%29%29<--->y-5=3%28x%2B2%29
A little algebra can be used to transform the equation above into the one and only slope-intercept form:
y-5=3%28x%2B2%29<--->y-5=3%28x%2B2%29<--->y-5=3%28x%2B2%29<--->y-5=3%28x%2B2%29
However, that is not necessary. The x- and y-intercepts can be found by making y=0 and x=0 respectively.
For that line,
the point on the x-axis, with y=0 , has
0-5=3%28x%2B2%29<--->-5=3%28x%2B2%29<--->-5%2F3=x%2B2<--->-5%2F3-2=x<--->x=-11%2F3 , and
the point on the y-axis, with x=0 , has
y-5=3%280%2B2%29<--->y-5=3%2A2<--->y-5=6<--->y=6%2B5<--->y=11 .
So the other end-point of the segment, on a coordinate axis is either
A%28-11%2F3%2C0%29 on the x-axis, or
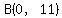B%280%2C11%29 on the y-axis.