SOLUTION: Find the equation for a hyperbola with eccentricity 3/2 and directrix x=2

The easiest hyperbola with directrix x=2 and eccentricity 3/2
is found by taking the focus to be the origin.



We take an arbitrary point (x,y) on the hyperbola, and, (in blue)
draw one line from the arbitrary point (x,y) to the focus (0,0) and
another line directly to and perpendicular to the directrix x=2

The ratio of the two blue lines is equal to the eccentricity 3/2.

The horizontal blue line has length |2-x|,

The slanted blue line has length 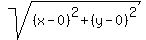 or


So we set their ratio equal to 3/2

 

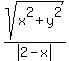
Square both sides













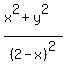
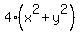
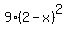
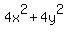
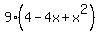
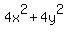
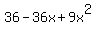
Edwin