Question 927442: 1.the sides of a triangle measures 20cm, 25,cm and 30 cm.
Find the length of the altitude to the shortest side.
Find the length of the median to the longest side.
find the length of the angle bisector of the smallest angle.
find the length of the line segment joining the midpoints of the 20-cm and 30-cm sides.
THANK YOUU.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.the sides of a triangle measures , , , and , and  . .
find the length of the angle bisector of the smallest angle.
find the length of the line segment joining the midpoints of the 20-cm and 30-cm sides.
Find the length of the altitude to the shortest side:
You know the lengths of 3 sides.
 , , , and , and 
h is the altitude
Use Heron's formula to find out the area
 ........where ........where = semi-perimeter and a,b, and c are side lengths = semi-perimeter and a,b, and c are side lengths




 then use then use


 ANSWER ANSWER
Find the length of the median to the longest side:
the longest side is 
Draw triangle  , with , with
 , ,  , , 
Using law of cosines, we get








Draw median from  to to  at point at point  . .
Now we have triangle 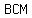 with with  , , 
We will find 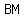 using law of cosines: using law of cosines:




Median  => =>  ANSWER ANSWER
find the length of the angle bisector of the smallest angle.
Then the length of the angle bisector  is given by: is given by:






 ANSWER ANSWER
find the length of the line segment joining the midpoints of the 20-cm and 30-cm sides.
The mid-segment of a triangle (also called a midline) is a segment joining the midpoints of two sides of a triangle.
Properties:
1.
The mid-segment of a triangle joins the midpoints of two sides of a triangle such that it is parallel to the third side of the triangle.
2.
The mid-segment of a triangle joins the midpoints of two sides of a triangle such that its length is half the length of the third side of the triangle.
so, the third side is 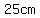 and the half of the third side is and the half of the third side is 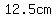 ANSWER ANSWER
|
|
|