SOLUTION: In the expansion of (x+y)n, the second term is 1620.the third term is 4320 and the fourth term is 5760,find the values of x,y and n

Algebra ->  Sequences-and-series -> SOLUTION: In the expansion of (x+y)n, the second term is 1620.the third term is 4320 and the fourth term is 5760,find the values of x,y and n      Log On


   

Question 926468: In the expansion of (x+y)n, the second term is 1620.the third term is 4320 and the fourth term is 5760,find the values of x,y and n
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
If you count the terms starting with 0 instead of 1, 
there are n terms, and the kth term is 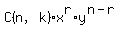C%28n%2Ck%29x%5Er%2Ay%5E%28n-r%29

In the expansion of (x+y)n, the second term is 1620.

That's the first term if you start counting with 0,  So

C%28n%2C1%29x%5En%2Ay%5E%28n-1%29=1620

n%2Ax%5En%2Ay=1620

the third term is 4320

That's the second term if you start counting with 0,  So

C%28n%2C2%29x%5E%28n-2%29%2Ay%5E2=4320

expr%28n%28n-1%29%2F2%29x%5E%28n-2%29%2Ay%5E2=4320 

n%28n-1%29x%5E%28n-2%29%2Ay%5E2=8640 

and the fourth term is 5760,

That's the third term if you start counting with 0,  So

C%28n%2C3%29x%5E%28n-3%29%2Ay%5E3=5760

expr%28n%28n-1%29%28n-2%29%2F6%29x%5E%28n-3%29%2Ay%5E3=5760

n%28n-1%29%28n-2%29x%5E%28n-3%29%2Ay%5E3=34560



Divide equal by equals. That is,

Divide the sides of the 2nd equation by the sides of the 1st equation

%28n%28n-1%29x%5E%28n-2%29y%5E2%29%2F%28n%2Ax%5E%28n-1%29%2Ay%29+=8640%2F1620

Simplify by canceling and subtracting exponents:

%28%28n-1%29y%29%2Fx=16%2F3
3%28n-1%29y=16x
3%28n-1%29%2F16=x%2Fy

Divide the sides of the 3rd equation by the sides of the 2nd equation



Simplify by canceling and subtracting exponents:

%28%28n-2%29y%29%2Fx=4
%28n-2%29y=4x
%28n-2%29%2F4=x%2Fy

Setting the expressions for x%2Fy equal

3%28n-1%29%2F16=%28n-2%29%2F4

multiply through by 16

3%28n-1%29=4%28n-2%29

3n-3=4n-8

5=n

Taking the first two equations of the system:

system%28n%2Ax%5E%28n-1%29%2Ay=1620%2Cn%28n-1%29x%5E%28n-2%29y%5E2=8640%29
system%285%2Ax%5E%285-1%29%2Ay=1620%2C5%285-1%29x%5E%285-2%29y%5E2=8640%29
system%285x%5E4%2Ay=1620%2C5%284%29x%5E3y%5E2=8640%29
system%285x%5E4%2Ay=1620%2C20x%5E3y%5E2=8640%29
system%28x%5E4%2Ay=324%2Cx%5E3y%5E2=432%29

Solve the 1st equation for y

y=324%2Fx%5E4
Substitute in the 2nd
x%5E3%28324%2Fx%5E4%29%5E2=432
x%5E3%28104976%2Fx%5E8%29=432
104976%2Fx%5E5=432
104976%2Fx%5E5=432
104976=432x%5E5
243=x%5E5
root%285%2C243%29=x
3=x
Substitute in
y=324%2Fx%5E4
y=324%2F3%5E4
y=324%2F81
y=4

So x=3, y=4, n=5 

Edwin