Question 926424: *Optimization problem*
Fencing is to be added to an existing wall of length 20 feet. How should the extra fence be added to maximize the area of the enclosed rectangle if the additional fence is: (state clearly how the extra fence is to be added)
a) 40 feet long?
b) 80 feet long?
c) 60 feet long?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Question 926424
COMMON SENSE THINKING:
Joe Sixpack, a carpenter by trade, would say that, obviously,
since you get the 20 feet of wall for free, you'd better use all 20 feet of it.
So, if you are going to add 40 ft of fence to form a rectangular enclosure,
obviously 20 feet will be parallel to the wall,
and the other  feet of fencing would form two 10-foot sides perpendicular to the wall. feet of fencing would form two 10-foot sides perpendicular to the wall.
Joe would similarly calculate that
with 80 feet of fencing,
you would use 20 feet for the side parallel to the wall,
and make the other two sides 30 feet long each, and
with 60 feet of fencing,
you would use 20 feet for the side parallel to the wall,
and make the other two sides 20 feet long each.
Luckily, Joe is right:

Maybe it is not so much luck,
but the fact that Joe has the horse sense you develop by making sure your handiwork fits in the space you have.
Joe would not have insisted on using the whole length of wall for very short lengths of fencing. He is smart enough to realize that a long and narrow rectangle along the wall does not give the maximum enclosure area.
He may even have checked his answers by increasing and decreasing the lengths of the sides perpendicular to the wall by 1 foot to make sure the changes did not increase the area.
THE ALGEBRA WAY TO THE SOLUTION:
 = length of wall used (in feet) = length of fence parallel to the wall. = length of wall used (in feet) = length of fence parallel to the wall.
 = length of each side of the rectangle perpendicular to the wall (in feet). = length of each side of the rectangle perpendicular to the wall (in feet).
 = total length of fencing available. = total length of fencing available.
 We know that We know that  <---> <---> <---> <--->
Enclosure  <---> <--->
That is a quadratic function of  , ,
like  . .
We know that when the leading coefficient is negative, 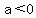 , ,
the function has a maximum for 
In the case of  , ,
there is a maximum when  . .
For 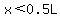 the function is increasing, and for the function is increasing, and for 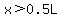 the function is decreasing. the function is decreasing.
a) For  , the maximum is at , the maximum is at
 --> --> --> --> --> --> --> --> . .
b) For  , the function is , the function is
 , or more specifically , or more specifically 

The function has a maximum at
 --> --> , ,
and it increases for 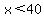 up to that maximum. up to that maximum.
In the available range of  , ,
the maximum is at  --> --> --> --> --> -->
c) For  , the function has a maximum at , the function has a maximum at
 --> --> , ,
and it increases for 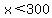 up to that maximum. up to that maximum.
In the available range of  , ,
the maximum is at  --> --> --> --> --> --> . .
Those answers are just like Joe Sixpack thought.
However, if the length of fencing available had been  , ,
the maximum of the area function would have been at
 with with  and and  , ,
and not at  with with  and and  , ,
as Joe may have expected.
|
|
|