Question 926384: I have no idea whatsoever how to do this, and the book is no help at all (gives one example, and it's unclear). Would someone please direct me to an explanation so that I can calculate these? I have many to do, so pointing me to good directions would be extremely helpful.
Let R be the relation on the set {1, 2, 3, 4, 5} containing the ordered pairs (1, 1), (1, 2), (1, 3), (2, 3), (2, 4), (3, 1), (3, 4), (3, 5), (4, 2), (4, 5), (5, 1), (5, 2), and (5, 4).
Find 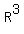 . .
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since R contains 13 elements, all ordered pairs, 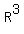 will contain
133 = 2,197 elements, all ordered triples of the ordered pairs
of R. So they will all be of the form will contain
133 = 2,197 elements, all ordered triples of the ordered pairs
of R. So they will all be of the form
 where (a,b), (c,d), (e,f) ∈ R
So you could write
where (a,b), (c,d), (e,f) ∈ R
So you could write 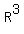 in set-builder notation this way: in set-builder notation this way:
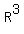  { {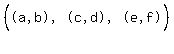 | (a,b), (c,d), (e,f) ∈ R}
Your teacher may accept just this simple form:
{(x,y,z)|x,y,z∈R}.
You'll have to ask your teacher what form he wants.
Edwin | (a,b), (c,d), (e,f) ∈ R}
Your teacher may accept just this simple form:
{(x,y,z)|x,y,z∈R}.
You'll have to ask your teacher what form he wants.
Edwin
|
|
|