Question 926264: Given the points A(-2, 1) and B(4, 5), determine the coordinates of point P on directed line segment that partitions in the ratio 7/3.
A 7/3 ratio divides the segment into equal parts.
The direction is from A to B, so use the ratio k from A/P which is of the line segment.
Find the rise and the run of .
The x-coordinate of P is x1 + k • run =
The y-coordinate of P is y1 + k • rise =
The coordinates of P are (, )
Answer by Edwin McCravy(20064)   (Show Source):
You can put this solution on YOUR website! Given the points A(-2, 1) and B(4, 5), determine the coordinates of point P on directed line segment that partitions in the ratio 7/3.
  
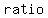The ratio of the parts is not k. We calculate k this way:
  
That is, to find k we must add the numerator to the denominator of the
ratio of the two parts. We plot the point and draw the line connecting them,
guessing about where P(?,?) might be:
Now we draw the run (in green) and the rise (in red):
Now we count the blocks and find that the green RUN is 6 units long
and that the red RISE is 4 units long.
Now since we know the RUN=6 and the RISE=4, and that
k = 7/10, x1=[x-coordinate of A]=-2, y1=[y-coordinate of A]=1, we are
ready to substitute:
The x-coordinate of P is x1 + k • run = -2 + 7/10 • 6 =
-2 + 42/10 = -2 + 21/5 = -10/5 + 21/5 = 11/5
The y-coordinate of P is y1 + k • rise = 1 + 7/10 • 4 =
1 + 28/10 = 1 + 14/5 = 5/5 + 14/5 = 19/5
The coordinates of P are (11/5,19/5). Final graph:
Edwin
|
|
|
