SOLUTION: Please help! I need step by step help on solving this equation. There are three parts to it. The following equation describes a circle: x^2+(y-3)^2=16 a) What is the radius of

What he told you is right.  Here's something else you can do:

Make a table of values:

 x | y
 -----
   |-1
 4 |
-4 |
   | 7

Substitute to finish the table:

   x²+(y-3)²=16    x²+(y-3)²=16     x²+(y-3)²=16   x²+(y-3)²=16 
  x²+(-1-3)²=16    4²+(y-3)²=16  (-4)²+(y-3)²=16   x²+(7-3)²=16 
    x²+(-4)²=16    16+(y-3)²=16     16+(y-3)²=16       x²+4²=16
       x²+16=16       (y-3)²=0         (y-3)²=0        x²+16=16
           y=0           y-3=0            y-3=0           x²=0
                           y=3              y=3            x=0

So we fill in the table:

 x | y
 -----
 0 |-1
 4 | 3
-4 | 3
 0 | 7

We plot those 4 points (0,-1), (4,3), (-4,3), (0,7)



Let's connect (-4,3) and (4,3) and also connect (0,-1) and (0,7).
We can tell they have to be two diameters:



  
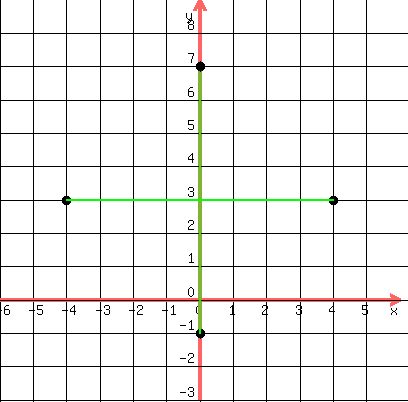Now we can easily tell what the center is.  It's that red point where 
those two green diameters cross. It's half-way between the points (-4,3)
and (4,3) and also halfway between the other two points we plotted.  So 
the center is the red point (0,3).  We can count the units and see that 
the radius is 4 units from the red center to each of those four points.



So now we can take our compass, open it up 4 units, put the sharp point
at (0,3), and swing out this circle:



Now notice that you could have told by looking at the equation:

x²+(y-3)²=16

Write the x as (x-0)

(x-0)²+(y-3)²=16

See the -0 and the -3?  Change their signs and you have 0, and 3, 
so the center is (0,3).

See the 16?  Take its square root.  That's 4 because 4 squared (or 4 times 4) is 16.
That tells us that the radius is 4.

So we can look at the standard equation of a circle:

(x-h)2+(y-k)2=r2

change the sign of what follows the x and the y, and that will be
the coordinates of the center.  Then take the square root of what is
after the equal sign and that will be the radius.

Edwin