Question 925613: If one root of the equation x^2-12x-P=0 is the square of the other, then find the value of P?
Found 3 solutions by josgarithmetic, Edwin McCravy, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
That's one way of solving it. Here's another.
Either way you'll have to check for extraneous solutions.
Let the two roots be x=a and x=b,
Then we have a system of three equations and 3 unknowns:
 Substitute
Substitute  for for  in in


 Solve for P
Solve for P
 Substitute in
Substitute in





 It's easy to see that 1 is a solution to
It's easy to see that 1 is a solution to  1 | 1 0 -13 12
| 1 1 -12
1 1 -12 0
So we have factored the polynomial equation as
1 | 1 0 -13 12
| 1 1 -12
1 1 -12 0
So we have factored the polynomial equation as
 We further factor it as
We further factor it as
 So we have four solutions for a
a=0, a=1, a=-4, a=3
although one or more may be extraneous.
Substituting a=0 in
So we have four solutions for a
a=0, a=1, a=-4, a=3
although one or more may be extraneous.
Substituting a=0 in


 Substituting a=1 in
Substituting a=1 in



 Substituting a=-4 in
Substituting a=-4 in




 Substituting a=3 in
Substituting a=3 in




 ------------------
Checking:
P=0
------------------
Checking:
P=0




 , ,  So P=0 is extraneous
P=-11
So P=0 is extraneous
P=-11




 , ,  So P=-11 is extraneous
P=64
So P=-11 is extraneous
P=64



 , ,  P=64 is a solution, since (-4)2=16
P=-27
P=64 is a solution, since (-4)2=16
P=-27




 , ,  P=-27 is a solution, since 32=9
There are 2 actual solutions, P=64 and P=-27
Edwin
P=-27 is a solution, since 32=9
There are 2 actual solutions, P=64 and P=-27
Edwin
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! If one root of the equation x^2-12x-P=0 is the square of the other, then find the value of P?

The roots’ sum:  ______ ______ , or 12 , or 12
Let smaller root be S
Then larger root = 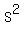
Since the 2 roots’ sum is 12, then we can say that: 

(S + 4)(S - 3) = 0
S, or smaller root = - 4, or 3
When smaller root = - 4, then larger root = 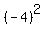 , or 16 , or 16
When smaller root = 3, then larger root =  , or 9 , or 9
The roots’ product:  ______ ______ , or – P , or – P
Roots’ product, when roots are – 4 and 16: - 4(16), or – 64
Thus, - P = - 64
 , or , or 
Roots’ product, when roots are 3 and 9 = 3(9), or 27
Thus, - P = 27
 , or , or 
|
|
|