You can
put this solution on YOUR website!
(3x - a)(x - 2)(x - 7) = 3x³ - 32x² + 87x - 70
It must be true for every value of x, so pick any
value for x and substitute it. The easiest value
of x we can pick is 0, so let's substitute 0 for x:
(3·0 - a)(0 - 2)(0 - 7) = 3(0)³ - 32(0)² + 87(0) - 70
(-a)(-2)(-7) = -70
-14a = -70
a =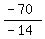 
a = 5
That's the answer. But you could have picked ANY number
to substitute for x. For example I could even have picked
a stupid number like 8
(3x - a)(x - 2)(x - 7) = 3x³ - 32x² + 87x - 70
(3·8 - a)(8 - 2)(8 - 7) = 3(8)³ - 32(8)² + 87(8) - 70
(24 - a)(6)(1) = 3(512) - 32(64) + 696 - 70
(24 - a)(6) = 1536 - 2048 + 626
6(24 - a) = 114
Divide both sides by 6
24 - a = 19
-a = 19-24
-a = -5
a = 5
Edwin
