Question 925315: Wesley measured all the interior angles in a polygon.he added them up to 991 degrees but he had missed out one angle. What type of polygon did Wesley measure? What is the size of the missing angle?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The  angles of a polygon with angles of a polygon with  sides add up to sides add up to 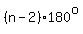 (see NOTE below). (see NOTE below).
So, for  , the sum of the angle measures is , the sum of the angle measures is  , ,
for  , the sum of the angle measures is , the sum of the angle measures is  , and , and
for  , the sum of the angle measures is , the sum of the angle measures is  . .
The missing angle could measure
 if it was a polygon with if it was a polygon with  sides, sides,
and that is a very reasonable solution.
Wesley measured a polygon with 8 sides, an  . .
The numbers do not work out for less sides or more sides.
For  , the sum of the angle measures would be at most , the sum of the angle measures would be at most 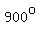 , which is less than , which is less than 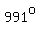 . .
For  , the missing angle would have to measure at least , the missing angle would have to measure at least  , ,
and that would make it a convex polygon, something your teacher does not expect:

NOTE: A triangle has  sides, and sides, and  interior angles whose measures add up to interior angles whose measures add up to  : :  . .
Attaching another triangle with a common side you gain 1 extra side, and get a quadrilateral, like the kite below:
 , with , with  sides, and sides, and  angles whose measures add up to angles whose measures add up to  . .
Repeating the process we get a pentagon,
with  sides, and sides, and  angles whose measures add up to angles whose measures add up to  , ,
and repeating the process once more we get a hexagon,
with  sides, and sides, and  angles whose measures add up to angles whose measures add up to  : :
 and and  Following the pattern, the Following the pattern, the  angles of a polygon with angles of a polygon with  sides add up to sides add up to 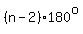
This is not a proof, but I thought it was a good way to remember the formula.
|
|
|