Question 92503: Scenario:
You need to make a round trip from Dallas to Ft. Worth (total distance 60 miles), and you want to average 60 miles an hour for your trip.
Problem:
Traffic is heavy on the Dallas to Ft. Worth leg of your trip and you are only able to average 30 miles per hour
How fast must you travel on the return leg in order to average 60 miles an hour for the entire trip?
Ft. Worth to Dallas 30 miles
Dallas to Ft. Worth 30 miles
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!
You need to make a round trip from Dallas to Ft. Worth (total distance 60 miles), and you want to average 60 miles an hour for your trip.
`
`
Problem:
Traffic is heavy on the Dallas to Ft. Worth leg of your trip and you are only able to average 30 miles per hour
`
How fast must you travel on the return leg in order to average 60 miles an hour for the entire trip?
`
`
Ft. Worth to Dallas 30 miles
Dallas to Ft. Worth 30 miles
`
Wow! You're just going there, turn around and come back. Then why go? Just to burn gas? Haha! Just joking.
On the serious side:
This is impossible because to average 60 mph you must go the entire 60 miles in 1 hour. However if you went 30 miles at 30 mph you have already used up the WHOLE HOUR!!, and you would need to already be back in Dallas at the end of that hour, but instead you are only in Ft. Worth. You cannot possibly have gone 60 miles at the end of that hour if you have only gone 30 miles at the end of that hour.
`
But let's pretend we weren't smart enough to notice that
it's impossible and tried to solve it anyway.
Make this DRT-chart (pronounced "dirt"-chart)
DISTANCE RATE TIME
D to FtW
FtW to D
Let's let x be the answer to the problem, that is, the
rate at which he must travel to achieve the goal of
having averaged 60 mph.
DISTANCE RATE TIME
D to FtW
FtW to D x
Now the slow rate he had to travel when going from
D to FtW is 30 mph, so let's fill that in for the
rate going
DISTANCE RATE TIME
D to FtW 30
FtW to D x
Now we are told the two distances are 30 miles going
and 30 miles coming. So fill in 30 for each of the
distances:
DISTANCE RATE TIME
D to FtW 30 30
FtW to D 30 x
Next use the formula 
to fill in the two times:
DISTANCE RATE TIME
D to FtW 30 30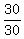 
FtW to D 30 x 
Reducing the 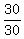to just 1
DISTANCE RATE TIME
D to FtW 30 30 1
FtW to D 30 x
Now we use the formula
TOTAL DISTANCE
AVERAGE RATE = 覧覧覧覧覧覧覧覧
TOTAL TIME
To get the TOTAL DISTANCE, we add the two DISTANCEs,
30 miles going + 30 miles coming and that = 60 miles.
To get the TOTAL TIME, we add the two TIMEs, 1 +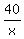 
For the AVERAGE RATE we substitute 60 mph.
So the equation is:
 = 
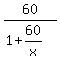Write the left side as a fraction with 1 denominator:
 =
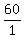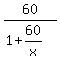Now we can cross-multiply and get
 = 
=
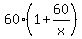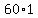
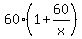Divide both sides by 60
 = 
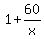Subtract 1 from both sides:
 = 
Multiply both sides by x
=
I don't think those are equal, do you? Haha! I think
60 is a lots bigger than 0. So if this problem has
a solution, then 60 must equal to 0. But since 60
doesn't equal 0, there can't be any solution to the
problem.
So that's what you have to do if you can't reason out
that the 1-hour span of time, that he must have been
able to go 60 miles in, had already passed, and he's
only done 30 miles in it, so it's too late for him to
average 60 mph on the round trip.
Edwin
|
|
|
