Question 924878: 1. In isosceles triangle LKM, with vertex angle K (figure shown below), answer the following questions:
a. If LK = 2x – 10, KM = 24 and LM = 12, solve for x.
b. If angle K = 40°, find the measure of angle L.
(5 points)
Score
2. In triangle PQR, if PQ = 21 cm and QR = 5 cm, then answer the following questions.
a. Is it possible to have PR = 20?
b. Is it possible to have PR = 26?
c. What are the possible lengths for PR ?
3. Determine the method that could be used to show the triangles ABC and CDA are congruent (SSS, SAS, ASA, AAS or Not Congruent):
a.
b.
c.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1. In isosceles triangle LKM, with vertex angle K (figure shown below), answer the following questions:
an isosceles triangle has two equal sides
since I see no figure, I will choose the vertex angle  be the point where equal sides be the point where equal sides 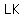 and and 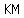 meet, and meet, and  is base is base
a. If  , ,  and LM = 12, solve for x. and LM = 12, solve for x.
if  , then , then
 ...solve for ...solve for 



b. If angle  °, find the measure of angle °, find the measure of angle  . .
in an isosceles triangle angle  and angle and angle  are same: are same:
so, 


2. In triangle 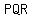 , if , if  and and  , then answer the following questions. , then answer the following questions.
a. Is it possible to have  ? ?
we know that in triangle one side is always less then the sum of other two sides:
so, 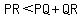
check, plug in given values
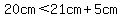
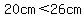 ...this is true, so it is possible to have ...this is true, so it is possible to have 
b. Is it possible to have  ? ?
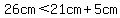
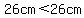 ...this is ...this is  true, so it is true, so it is  possible to have possible to have 
c. What are the possible lengths for  ? ?
the possible lengths for  : :  to to 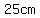
3. Determine the method that could be used to show the triangles ABC and CDA are congruent (SSS, SAS, ASA, AAS or Not Congruent):
it's really important to see figure here, without it I can't give you an answer
you can see what you are given and try to answer:
SSS- Side Side Side postulate states that if three sides of one triangle are congruent to three sides of another triangle, then these two triangles are congruent.
SAS- The Side Angle Side postulate (often abbreviated as SAS) states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent.
ASA- If two angles and the included side are congruent,then these two triangles are congruent.
AAS- The Angle Angle Side postulate (often abbreviated as AAS) states that if two angles and the non-included side one triangle are congruent to two angles and the non-included angle of another triangle, then these two triangles are congruent.
the are Not Congruent if they do not have any of above
a.
b.
c.
|
|
|