SOLUTION: 5) Find the value of S=(1/1!)+(3/2!)+(7/3!)+(13/4!)+(21/5!)+(31/6!)+(43/7!)+...... [Given that e^x = 1+(x/1!)+(x^2/2!)+.....] A. 2e+2 B. 3e-2 C. 2e-1 D. 2e+1

given:  (I hope you understand sigma summation notation)



Therefore



--------------------------------------------------------

We need first to find the nth term of the sequence of the numerators,

The sequence of numerators is 1,3,7,13,21,31,43,... 

They are all odd. Perhaps if we subtract 1 from each, 
we might recognize a pattern,

That would be the sequence 0,2,6,12,20,30,42.  Aha! That
pattern is 1*0,2*1,3*2,4*3,5*4,6*5,7*6 so its nth term is n(n-1)

So the nth term of the numerators is 1 more than that, or n(n-1)+1 

and

 becomes



That has an n(n-1) term on top, and we notice that if n≧2, n! can be written
n(n-1)(n-2)! which has that factor.  So let's write out the first term of S,
which is  so we can start the sum at n=2 instead of n=1, so,





(1)   

The first summation in (1) above:



we substitute n-2=k and n=k+2, and it becomes

.

The other summation in (1) above:

 is the summation for e except for the first two terms 
where n=0 and n=1.  Therefore,



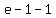
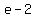Therefore (1) above becomes

(1)   1 + e + e-2 = 2e-1

The correct choice is C.

Edwin