|
Question 923827: Compound interest and logs.
I have seen a few similar questions but it is the twist in mine that is really confusing me.
Q: $50000 is deposited into an account with a 2% interest compounded annually.
If a sum equivalent to half the previous years interest is withdrawn every year:
a) What year will she take out $550
b) How long will it take until $6000 has been withdrawn.
I have the answers by doing it in baby steps : i.e calculating interest , dividing it by half and adding it to initial total. and did this for 11 years, where she will withdraw $552.31, and then also know that it should be 12 years till $6000 has withdrawn.
I would love help with a formula that works that takes into consideration half the previous year interest withdrawn. Thanks in advance :)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! it's not clear whether you are dealing with a present balance of $5,000 or $50,000
I'll show you what I get with both so you can see what i mean.
my numbers don't agree with yours.
the assumption is that the account grows by 2% every year and that you withdraw half of the interest each year.
this means that you keep half of the interest every year in the account.
half of 2% is equal to 1%.
your account is therefore growing at an effective annual rate of 1% per year since 1% of the interest is kept in the account each year.
the other 1% is withdrawn and does not grow with the account.
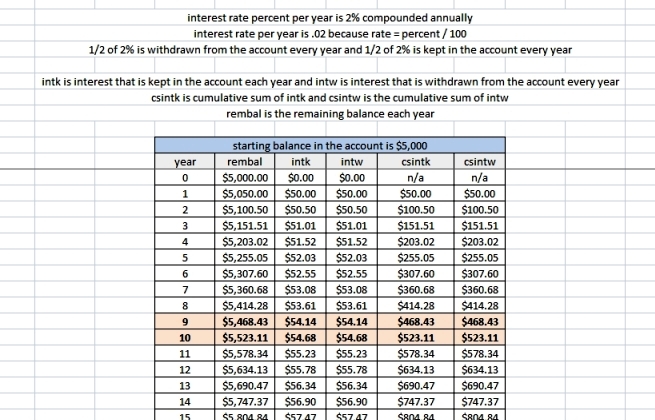
i did a year by analysis using excel.
it shows you the interest kept and withdrawn from the acocunt each year plus the cumulative sum of that interest.
intk is 1% interest that is kept in the account.
intw is 1% interest that is withdrawn from the account.
csintk is the cumulative sum of intk
csintw is the cumulative sum of intw
csintk tells you the total interest that remains in the account after n years.
csintw tells you the total interest that has been withdrawn from the account after n year.
i first did it assuming $5,000 was the principal.
the total amount of interest withdrawn from the account became $500 sometime between year 9 and 10.
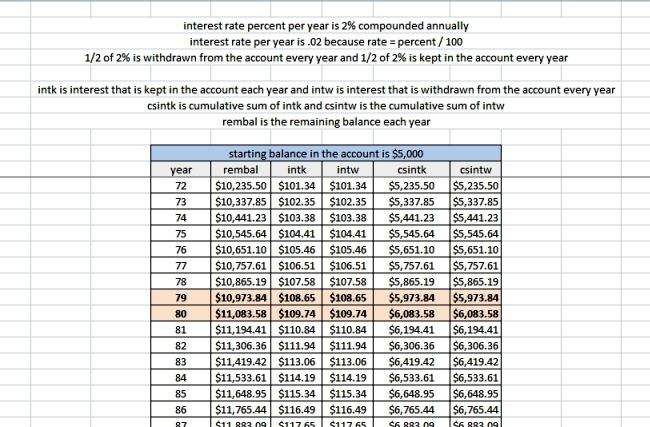
the total amount of interest withdrawn from the account became $6000 sometime between year 79 and 80.
you can see those results in the following 2 pictures.
i then did it assuming $50,000 was the principal.
the total amount of interest withdrawn from the account became $500 in year 1 which is the first year that interest is accrued.
this is because .02 * $50,000 = $1,000 and half is kept in the account and half is withdrawn from the account. that's $500 kept and $500 withdrawn.
the total amount of interest withdrawn from the account became $6000 sometime between year 11 and 12.
you can see those results in the next picture.

there is a formula to calculate it but it's not as straightforward as you might think.
what you have to do is use the formula to calculate for the interest that is kept in the account after n years.
once you get that, you automatically have the year for the interest that is withdrawn from the account after that same number of years.
your problem is actually simplified because you withdrew the same amount that you kept in the account.
the problem becomes more complicated if you keep a different amount than you withdraw.
i will show you how to do the calculation.
the formula to use is:
f = p * (1+i)^n
that gives you the future value of the investment.
to find the interest you have to subtract the principal.
you get:
fi = p * (1+i)^n - p
in this formula:
fi is the interest that is kept in the account after n years.
this is an important point.
it's the interest that is kept in the account after n years, not the interest that is withdrawn.
p is the principal which is the initial investment.
i is the effective interest rate for the part of the interest that is kept in the account.
another important point.
it's the interest rate of the interest that is kept in the account after n year, not the interest rate of the interest that is withdrawn.
n is the number of year.
as i said before, your problem is simplified because the interest that is kept in the account is the same as the interest that is withdrawn from the account.
that makes your problem simple because all you have to do is calculate the interest that is kept in the account and you automatically have the interest that is withdrawn from the account because they are the same.
bottom line is that the following calculation only works if the interest kept in the account is the same as the interest withdrawn from the account each year.
the formula is fi = p * (1 + i) ^ n - p
fi is the interest that you want to have kept in the account after n years.
that is $500 for the first analysis and $6000 for the second analysis.
i will do the analysis assuming $5,000 is the principal and $500 is the amount of interest that is kept in the account after n years.
i'll leave you to do the other analyses using the same method.
first analysis assumes $500 is kept in the account after n years.
fi = p * (1 + i) ^ n - p becomes:
500 = 5,000 * (1.01) ^ n - 5,000
the interest rate is the interest rate that is kept which is 1/2 of 2% which becomes 1% which becomes a rate of .01.
the interest is the interest that is kept in the account after n years.
it just happens to be the same as the interest that is withdrawn from the account after n year.
that only happens if they interest withdrawn is equal to the interest kept.
you need to solve for n.
add 5,000 to both sides of the equation to get:
5,500 = 5,000 * (1.01)^n
divide both sides of the equation by 5,000 to get:
5,500 / 5,000 = (1.01)^n
take the log of both sides of the equation to get:
log(5,500/5,000) = log(1.01^n)
since log(1.01^n) is the same as n * log(1.01), your equation becomes:
log(5,500/5,000) = n * log(1.01)
divide both sides of this equation by log(1.01) to get:
log(5,500/5,000) / log(1.01) = n
solve for n to get:
n = 9.57859404
the amount of interest that is kept in the account will reach $500.00 in 9.57859404 years.
that's between the 9th and the 10th year.
that agrees with the detailed year by year analysis.
since the interest that is kept in the account is the same as the interest that is withdrawn from the account, then you also have the year in which $500.000 interest was withdrawn from the account.
once again, this only works if the interest that is withdrawn from the account is the same as the interest that is kept in the account.
if they're different, then it's more complicated.
it's more complicated because you have to calculate the interest rate of the interest that is withdrawn from the account and the interest rate that is kept in the account.
you then have to use the interest rate for the interest that is kept in the account.
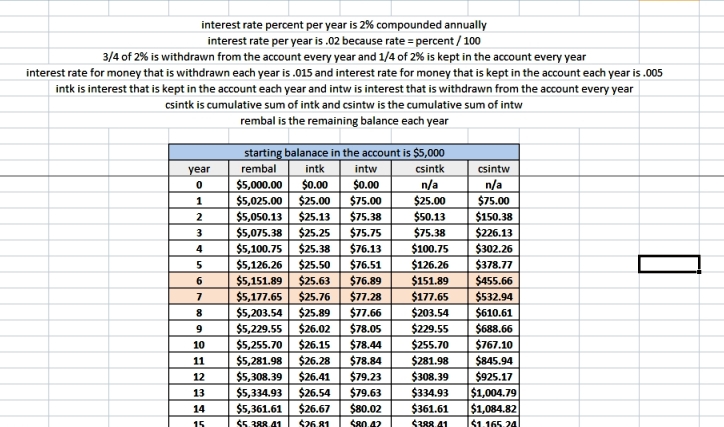
for example, assuming 2% interest is the total interest per year and you keep 1/4 of the interest in the account and you withdraw 3/4 of the interest each year.
the interest rate for the interest that is kept in the account is now 1/4 * 2% = .5% and the interest rate for the interest that is withdrawn from the account is now 3/4 * 2% = 1.5%.
the interest rate that has to be used is in the interest rate for the interest that is kept in the account.
now if you want to find the year in which $500 was withdrawn from the account, you need to calculate the equivalent amount of interest that remains in the account in that same year.
since you withdraw 3/4 of the interest each year, then you keep 1/4 of the interest each year.
in year n you have withdrawn 500.
500 is 3/4 of the total interest so if you multiply 500 by 4/3 you will get the total interest in year n.
500 * 4/3 = 666.6666.....
this is the total interest year in year n.
1/4 of that is equal to 166.666.... which i'll round to 167.
you want to find the year in which the interest that is kept in the account is equal to 167.
that same year will be the year in which 500 interest was withdrawn from the account.
the formula is, once again...
fi = p * (1 + i) ^ n - p
fi is equal to 166.67
p is equal to 5,000
i is equal to .005 which is 1/4 of .02 that was calculated before.
n is what you want to find.
the equation becomes:
167 = 5,000 * (1.005) ^ n - 5000
add 5000 to both sides of this equation to get:
5,167 = 5,000 * (1.005) ^ n
divide both sides of this equation by 5,000 to get:
5,167/5,000 = 1.005^n
solve for n to get:
n = 6.587280887
this is between the 6th and 7th year.
the year by year analysis of that is shown below.
it confirms that the year that 500 was withdrawn from the account is between year 6 and 7.
it also confirms that the year that 167 was kept in the account is between year 6 and 7 as well.
|
|
|
| |