|
Question 923755: I have been pounding my head for 2 days trying to figure out the right equation for this problem and I am hoping someone here can help.
What is the amount a person would have to deposit today to be able to take out $5000 a year for 10 years from an account earning 8 percent annually?
Thanks!
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! p, amount to deposit today.
YEAR_________________BAL
0___________________p(1.08)^0
1___________________p(1.08)^1
2___________________p(1.08)^2
y___________________p(1.08)^y
Your question asks,  to find p. to find p.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The way I understand it you want to know how much money should be deposited at time = 0 years,
into an account earning 8 percent annually,
so that at t=1 year, t=2 years, ..., t=8 years,
there would be at least $5000 that can be taken out.
At  , ,  . .
At  (at the end of the first year) 8% interest ( (at the end of the first year) 8% interest ( 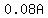 is added to the balance, is added to the balance,
bringing the balance up to  , ,
and immediately, 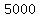 is taken out, is taken out,
bringing the balance down to 
At  , , 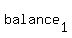 is again is again
increased by a factor of  , ,
and reduced by the withdrawal of 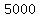 , so , so
 . .
At  , , 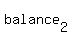 is again is again
increased by a factor of  , ,
and reduced by the withdrawal of 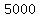 , so , so
 . .
This pattern repeats every year, and
at  , ,

If at that point  , ,





NOTE:
The sum 
is the sum of a geometric sequence with ratio  . .
You may know a formula for that, but otherwise you can see that
 , and then , and then
 ---> ---> ---> --->
|
|
|
| |