Question 923750: The average of n numbers is P. if the first
number is increased by 1, second by 2, third by
3 and so on, then their average becomes Q. the
value of Q-X is
(a) n/2+1
(b) n(n+1)/2
(c) n
(d) n+1/2
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website!
Did you mean Q - P? There is no X.
I'm going to assume you meant Q-P and NOT Q-X.
-------------------------------------------------------
We have a set of n numbers. I'm going to call them: x1, x2, x3, ..., xn
They sum to S = x1 + x2 + x3 + ... + xn
The average P is P = S/n
-------------------------------------------------------
Increase x1 by 1: x1+1
Increase x2 by 2: x2+2
Increase x3 by 3: x3+3
...
...
...
Increase xn by n: x3+n
Notice how the increases for {x1,x2,x3,...,xn} are given in this order: 1, 2, 3, ..., n
Add up those increases: 1+2+3+...+n = n*(n+1)/2. This is a well known identity.
-------------------------------------------------------
So we go from
x1 + x2 + x3 + ... + xn
to
(x1+1) + (x2+2) + (x3+3) + ... + (xn+n)
to
(x1 + x2 + x3 + ... + xn) + (1+2+3+...+n)
which turns into
S + n*(n+1)/2
We still have n numbers, so we divide that by n to get 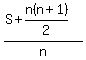 . This is the new average Q.
So...
|
|
|
