Lets start with the given system of linear equations


Now in order to solve this system by using substitution, we need to solve (or isolate) one variable. I'm going to choose y.
Solve for y for the first equation
 Subtract Subtract 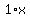 from both sides from both sides
 Divide both sides by 1. Divide both sides by 1.
Which breaks down and reduces to
 Now we've fully isolated y Now we've fully isolated y
Since y equals 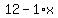 we can substitute the expression we can substitute the expression 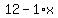 into y of the 2nd equation. This will eliminate y so we can solve for x. into y of the 2nd equation. This will eliminate y so we can solve for x.
 Replace y with Replace y with 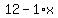 . Since this eliminates y, we can now solve for x. . Since this eliminates y, we can now solve for x.
 Distribute 1 to Distribute 1 to 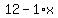
 Multiply Multiply
 Reduce any fractions Reduce any fractions
 Subtract Subtract  from both sides from both sides
 Combine the terms on the right side Combine the terms on the right side
 Now combine the terms on the left side. Now combine the terms on the left side.
 Multiply both sides by Multiply both sides by 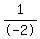 . This will cancel out . This will cancel out 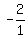 and isolate x and isolate x
So when we multiply 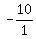 and and 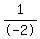 (and simplify) we get (and simplify) we get
 <---------------------------------One answer <---------------------------------One answer
Now that we know that  , lets substitute that in for x to solve for y , lets substitute that in for x to solve for y
 Plug in Plug in  into the 2nd equation into the 2nd equation
 Multiply Multiply
 Add Add  to both sides to both sides
 Combine the terms on the right side Combine the terms on the right side
 Multiply both sides by Multiply both sides by  . This will cancel out 1 on the left side. . This will cancel out 1 on the left side.
 Multiply the terms on the right side Multiply the terms on the right side
 Reduce Reduce
So this is the other answer
 <---------------------------------Other answer <---------------------------------Other answer
So our solution is
 and and 
which can also look like
( , , ) )
Notice if we graph the equations (if you need help with graphing, check out this solver)


we get
 graph of graph of  (red) and (red) and  (green) (hint: you may have to solve for y to graph these) intersecting at the blue circle. (green) (hint: you may have to solve for y to graph these) intersecting at the blue circle.
and we can see that the two equations intersect at ( , , ). This verifies our answer. ). This verifies our answer.
-----------------------------------------------------------------------------------------------
Check:
Plug in ( , , ) into the system of equations ) into the system of equations
Let  and and  . Now plug those values into the equation . Now plug those values into the equation 
 Plug in Plug in  and and 
 Multiply Multiply
 Add Add
 Reduce. Since this equation is true the solution works. Reduce. Since this equation is true the solution works.
So the solution ( , , ) satisfies ) satisfies 
Let  and and  . Now plug those values into the equation . Now plug those values into the equation 
 Plug in Plug in  and and 
 Multiply Multiply
 Add Add
 Reduce. Since this equation is true the solution works. Reduce. Since this equation is true the solution works.
So the solution ( , , ) satisfies ) satisfies 
Since the solution ( , , ) satisfies the system of equations ) satisfies the system of equations


this verifies our answer.
|