SOLUTION: Very confused here... Suppose csc t = 4 and tan t > 0 sin(t - 6π) = cot(5π-t) = cos(-t) = sin(2t) = cos(t+5π/3) = I am having confusion with a f

Algebra ->  Trigonometry-basics -> SOLUTION: Very confused here... Suppose csc t = 4 and tan t > 0 sin(t - 6π) = cot(5π-t) = cos(-t) = sin(2t) = cos(t+5π/3) = I am having confusion with a f      Log On


   

Question 922568: Very confused here...

Suppose csc t = 4 and tan t > 0
sin(t - 6π) =
cot(5π-t) =
cos(-t) =
sin(2t) =
cos(t+5π/3) =

I am having confusion with a few things. I know that I would use a right triangle in the first quadrant to find the missing adjacent angle. However, I posted this question early and was told that instead of using a^2 = c^2+b^2 for this it is a^2 = c^2 - b^2 which produces √15 as opposed to √17. I am even more confused after that because I don't understand what the pieces in the parentheses are asking me to do. Such as t-6π, 5π-t and so on.
Please explain how this works
THANKS
Found 2 solutions by josmiceli, Edwin McCravy:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
I think you're having trouble "reading" these functions
------------------
It helps if you can visualize the plot of +f%28t%29+ and +t+
for example,
+f%28t%29+=+sin%28+t+-+6pi+%29+
+6pi+ is called the phase angle
If you set +t+=+0+ then you have:
+f%280%29+=+sin%28+-6%2Api+%29+
+-6%2Api+=+-3%2A%28+2%2Api+%29+
This is a multiple of +2%2Api+, and since
+sin%28+2%2Api+%29+=+0+, then
+sin%28+-6%2Api+%29+=+0+
So, I have:
+f%280%29+=+0+
Here's the plot:
+graph%28+400%2C+400%2C+-10%2C+10%2C+-1.5%2C+1.5%2C+sin%28+x+-+6%2Api+%29%29+
As you can see, there is no difference between this
function and +sin%28t%29+
Now I can say:
+csc%28t%29+=+4+
+sin%28t%29+=+1%2F4+
+sin%28+t+-+6%2Api+%29+=+1%2F4+
-----------------------
You are correct that the angle whose csc is +4+
and whose tan is > 0 is in the 1st quadrant
+sin%28t%29+=+1%2F4+
If +a+=+1+
+c+=+4+ , then
+b+=+sqrt%28+4%5E2+-+1%5E2+%29+
+b+=+sqrt%28+15+%29+
----------------
Now note that +b%2Fc+=+cos%28t%29+
+c%2Fb+=+sec%28t%29+
Hope this helps a little -you just have to keep
testing yourself on what you are vague on



Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
You need to learn some trigonometric identities:

1.  sin(A+B) = sin(A)cos(B)+cos(A)sin(B)
2.  sin(A-B) = sin(A)cos(B)-cos(A)sin(B) 
3.  cos(A+B) = cos(A)cos(B)-sin(A)sin(B)
4.  cos(A-B) = cos(A)cos(B)+sin(A)sin(B)
5.  sec%28A%29=1%2Fcos%28A%29
5.  csc%28A%29=1%2Fsin%28A%29
6.  tan%28A%29=sin%28A%29%2Fcos%28A%29
7.  cot%28A%29=cos%28A%29%2Fsin%28A%29
8.  pi=%22180%B0%22
9.  sin%28n%2Api%29+=+0 for all integers n
10. cos%28n%2Api%29+=+1 for even integers n 
    cos%28n%2Api%29+=+-1 for odd integers n

Suppose csc t = 4 and tan t > 0 
4 is positive so csc is positive and tangent is positive,
so t is in quadrant 1.

The cosecant is 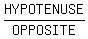HYPOTENUSE%2FOPPOSITE, so draw a right
triangle containing angle t.  Make the hypotenuse 4 and the 
side opposite angle t be 1.  Then csc(t) will be 4/1 or 4.



Since the hypotenuse = 4 and the opposite side = 1, then 

HYPOTENUSE%5E2=OPPOSITE%5E2%2BADJACENT%5E2
4%5E2=1%5E2%2BADJACENT%5E2
16=1%2BADJACENT%5E2
15=ADJACENT%5E2
sqrt%2815%29=ADJACENT

So we put 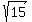sqrt%2815%29 on the adjacent side:

sin(t - 6π) =
First use 2 above.
sin%28t-6pi%29+=+sin%28t%29cos%286pi%29-cos%28t%29sin%286pi%29 
sin%28t-6pi%29+=+%281%2F4%29cos%286pi%29-%28sqrt%2815%29%2F4%29sin%286pi%29
Now use 9 and 10 above 
sin%28t-6pi%29+=+%281%2F4%29%281%29-%28sqrt%2815%29%2F4%29%280%29
sin%28t-6pi%29+=+1%2F4-0
sin%28t-6pi%29+=+1%2F4

cot(5π-t) = 
First use 7 above
cot%28A%29=cos%28A%29%2Fsin%28A%29 
cot%285pi-t%29=cos%285pi-t%29%2Fsin%285pi-t%29
Now use 4 and 2

Now use 9 and 10 and the right triangle to substitute for all the sines
and cosines

cot%285pi-t%29=%28-sqrt%2815%29%2F4%29%2F%281%2F4%29=-sqrt%2815%29+

cos(-t) = 
Write -t as 0-t and use 4

cos%28-t%29=cos%280-t%29+=+cos%280%29cos%28t%29%2Bsin%280%29sin%28t%29

Now use 9 and 10 and the right triangle to substitute for all the sines
and cosines

cos%28-t%29=cos%280-t%29+=+1%2Asqrt%2815%29%2F4%2B%280%29%281%2F4%29

cos%28-t%29=sqrt%2815%29%2F4

sin(2t) = 
Write 2t as t+t and use 1:



Use the right triangle above to substitute for the sines and cosines:

sin%282t%29=2%281%2F4%29%28sqrt%2815%29%2F4%29

sin%282t%29=%281%2F2%29%28sqrt%2815%29%2F4%29

sin%282t%29=%28sqrt%2815%29%2F8%29

cos(t+5π/3) =
Use 8

cos%28t%2B5pi%2F3%29=cos%28t%2B5%28%22180%B0%22%2F3%29%29=cos%28t%2B%22300%B0%22%29

Use 3



300° is one of the special angles in quadrant IV with reference angle 60°

cos%28%22300%B0%22%29=1%2F2, sin%28%22300%B0%22%29=-sqrt%283%29%2F2



cos%28t%2B5pi%2F3%29=sqrt%2815%29%2F8%2Bsqrt%283%29%2F8=%28sqrt%2815%29%2Bsqrt%283%29%29%2F8

Edwin