SOLUTION: A sequence of numbers is said to form a harmonic progression provided their reciprocals form an arithmetic progression. Insert three harmonic means between - 1/2 and 1/14.

Algebra ->  Sequences-and-series -> SOLUTION: A sequence of numbers is said to form a harmonic progression provided their reciprocals form an arithmetic progression. Insert three harmonic means between - 1/2 and 1/14.      Log On


   

Question 922288: A sequence of numbers is said to form a harmonic progression provided their reciprocals form an arithmetic progression. Insert three harmonic means between - 1/2 and 1/14.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I understand the first term to be the positive number 1%2F2 .
We need an arithmetic progression, where each term differs from the one before by a common difference d .
The first term is 2 , which is followed by 3 more terms, and then by 14 .
The terms are 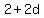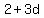2 , 2%2Bd , 2%2B2d , 2%2B3d , 14
The fifth term is 2%2B%285-1%29d=2%2B4d=14 .
2%2B4d=14--->4d=14-2--->4d=12--->d=12%2F4--->d=3 .
So the terms of the arithmetic progression are
2 , 2%2B3=5 , 5%2B3=8 , 8%2B3=11 , 11%2B3=14 ,
and the terms of the harmonic progression are
1%2F2 , 1%2F5 , 1%2F8 , 1%2F11 , and 1%2F14 .

NOTE: If the first term was -1%2F2 ,
then the arithmetic progression would be
-2 , 2 , 6 , 10 , 14 ,
and the harmonic progression would be
-1%2F2 , 1%2F2 , 1%2F6 , 1%2F10 , 1%2F14 .