 ,
, 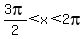 find
find
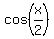 ,
,  , and
, and 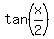 .
Since
.
Since 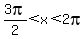 , dividing the three sides of the inequality by 2,
, dividing the three sides of the inequality by 2,
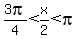 , which tells us that
, which tells us that  is in quadrant II
To find
is in quadrant II
To find 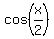 will need the half-angle formulas:
will need the half-angle formulas:
 But since
But since  is in quadrant II, its cosine is negative, so we
will only use the negative sign:
is in quadrant II, its cosine is negative, so we
will only use the negative sign:
 To simplify
To simplify  , multiply top and bottom by 5,
, multiply top and bottom by 5,  So
So  ---------------------
To find
---------------------
To find  will need the half-angle formulas:
will need the half-angle formulas:
 But since
But since  is in quadrant II, its sine is positive, so we
will only use the positive sign:
is in quadrant II, its sine is positive, so we
will only use the positive sign:
 To simplify
To simplify 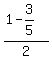 , multiply top and bottom by 5,
, multiply top and bottom by 5,  So
So  -------------------------
To find
-------------------------
To find 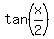 there are several half-angle identities we could
use.
there are several half-angle identities we could
use.
 However I think since I already have the sine and cosine of
However I think since I already have the sine and cosine of  ,
I'll use the quotient identity:
,
I'll use the quotient identity:
 Edwin
Edwin