|
Question 921634: Three machines A,B,C operating at the same time can do a job in 8 hours. If A alone operates for 2 hours and B alone for 3 hours, one-fourth of the job is done. Now if B alone operates for 5 hours and C alone for 14 hours, one-half of the job is done. How many hours would it take each to do the job alone?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Three machines A,B,C operating at the same time can do a job in 8 hours.
If A alone operates for 2 hours and B alone for 3 hours, one-fourth of the job is done.
Now if B alone operates for 5 hours and C alone for 14 hours, one-half of the job is done.
How many hours would it take each to do the job alone?
:
let a = time required by machine A alone
let b = time required by B
let c = time required by C
:
Write an equation for each statement.
:
let the completed job = 1
:
Three machines A,B,C operating at the same time can do a job in 8 hours.
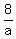 + + 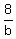 + + 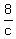 = 1 = 1
:
If A alone operates for 2 hours and B alone for 3 hours, one-fourth of the job is done.
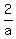 + + 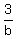 = = 
:
Now if B alone operates for 5 hours and C alone for 14 hours, one-half of the job is done.
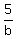 + + 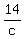 = = 
:
multiply the 2nd equation by 4, subtract from the 1st equation
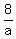 + + 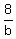 + + 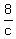 = 1 = 1
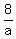 + +  + 0 = 1 + 0 = 1
---------------------------------subtraction eliminates a
0 -  + + 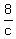 = 0 = 0
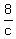 = = 
divide both sides 4
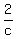 = = 
cross multiply
1c = 2b
in the 3rd original equation replace c with 2b
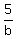 + + 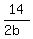 = = 
Reduce the fraction
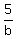 + + 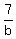 = = 
 = = 
b = 24 hrs working alone
then
c = 2(24)
c = 48 hrs alone
In the 2nd original equation, replace b with 24
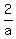 + +  = = 
reduce fraction
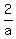 + +  = = 
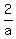 = =  - - 
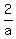 = = 
a = 16 hrs working alone
:
:
You can confirm this yourself using the 1st equation
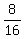 + + 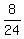 + + 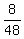 = 1 = 1
|
|
|
| |