Question 920473: A boat, whose speed in still water is x miles per hour, travels in a 5mph current, 75 miles downstream then 75 miles upstream. This takes 7 hours, 15 minutes. How fast is x?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A boat, whose speed in still water is x miles per hour, travels in a 5mph current, 75 miles downstream then 75 miles upstream.
This takes 7 hours, 15 minutes. How fast is x?
:
Change 7 hr 15 min to 7.25 hrs
:
(x+5) = effective speed downstream
and
(x-5) = effective speed upstream
:
Write a time equation; time = dist/speed
up time + down time = 7.25 hrs
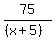 + + 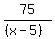 = 7.25 = 7.25
multiply by (x+5)(x-5), cancel the denominators and you have
75(x-5) + 75(x+5) = 7.25(x+5)(x-5)
75x - 375 + 75x - 375 = 7.25(x^2 - 25)
150x = 7.25x^2 - 181.25
Form a quadratic equation on the right
0 = 7.25x^2 - 150x - 181.25
Use the quadratic formula to find x, I got a positive solution of:
x = 21.8 mph in still water
:
:
See if that checks out, find the actual times each way, using the current of 5 mph.
75/26.8 = 2.80 hrs
75/16.8 = 4.46 hrs
--------------------
total time; 7.26 hrs, close anyway
|
|
|