Question 91926This question is from textbook Begining Algebra
: Hello,
Would you please help me with this problem:
Identify the axis of symetry, create a suitable table of values, and sketch th graph. y=-x^2+6x-2
This is how far I have gotten, but I am not too sure if I have gotten this part right.
y=-x^2+6x-2
y+2=-x^2+6x
y+2+9=x^2+6x+9
y+11=(x+3)^2
Can you please walk me through how to complete this type of problem?
This question is from textbook Begining Algebra
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!  Start with the given quadratic Start with the given quadratic
 Add Add  to both sides to both sides
 Factor out the leading coefficient Factor out the leading coefficient 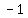 . This step is important since we want the . This step is important since we want the  coefficient to be 1. This is where you made your mistake coefficient to be 1. This is where you made your mistake
Take half of the x coefficient  to get to get  (ie (ie  ) )
Now square  to get to get  (ie (ie  ) )
 Add this number ( Add this number ( ) to the expression inside the parenthesis. ) to the expression inside the parenthesis.
 Since we added Since we added  inside the parenthesis, we need to add inside the parenthesis, we need to add 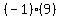 to the other side (remember, we factored out the leading coefficient to the other side (remember, we factored out the leading coefficient  ). ).
 Factor Factor  into into  . Now the right side is a perfect square (note: if you need help with factoring, check out this solver) . Now the right side is a perfect square (note: if you need help with factoring, check out this solver)
 Multiply Multiply  and and  to get to get  . .
 Combine like terms Combine like terms
 Add Add 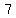 to both sides to isolate y to both sides to isolate y
--------------------------------------------------------------------------------
Now the quadratic  is in vertex form is in vertex form  where where  , ,  , and , and 
Remember, for any quadratic in vertex form  the vertex is (h,k) and the axis of symmetry is x=h the vertex is (h,k) and the axis of symmetry is x=h
So the vertex is ( , , ) and the axis of symmetry is x=3 ) and the axis of symmetry is x=3
-----------------------------------------------------------------------
In order to create a table of suitable values, simply plug in x-values that are close to the axis of symmetry.
For instance, plug in x=1 (which is two units away from the axis of symmetry) to get y=3. So our first point is (1,3)
Now plug in x=2 (which is one unit away from the axis of symmetry) to get y=6. That makes our second point (2,6).
Since we know the vertex is (3,7), our third point is (3,7)
Since the graph is symmetric with respect to the axis of symmetry, the x-value that is one unit to the right of the axis of symmetry (x=4) will have the same y-value as x=2 (since x=2 is also one unit away from the axis of symmetry). So our fourth point is (4,6)
Also the x-value that is two units to the right of the axis of symmetry (x=5) will have the same y-value as x=1 (since x=1 is also two units away from the axis of symmetry). This makes our fifth point at (5,3)
So our table looks like
| | | |
| 1 | | | 3 |
| 2 | | | 6 |
| 3 | | | 7 |
| 4 | | | 6 |
| 5 | | | 3 |
Now plot the points

Now connect the points to graph 

|
|
|