Question 919228: A bracelet that is supposed to be 18-Karat Gold weighs 238 grams. Gold weighs 19.3 grams per cubic centimeter. Copper weights 9 grams per cubic centimeter. The volume of the bracelet is 15 cubic centimeters of gold and copper.
Is the bracelet 18-Karat Gold? - I found out that it wasn't, but i have to use the substitution method to figure it out, but I don't know how to.
Thanks in advance (:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! WHAT YOUR TEACHER/TEXTBOOK THINKS:
18K gold is a mixture of 18 parts by volume of gold and 6 parts by volume of something else (or 75 % gold by volume and 25% other stuff by volume). Volumes mixed add, and so do masses.
 = volume of gold in cubic centimeters
 = volume of copper in cubic centimeters
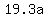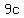 = mass of gold in grams
 = mass of copper in grams
So  is their system.
Their solution by substitution could be
solving  for ,
---> ,
and substituting into  :
Since 10 cubic centimeters is less that 75% of 15 cubic centimeters,
which is  cubic centimeters,
your teacher textbook concludes that it is nor 18k gold, but less than 18k.
The ratio  is the ratio that corresponds to 16k gold.
Unfortunately 18K gold is 75% by weight, not by volume, so the problem has uglier numbers and the conclusion is different.
A CHEMIST'S POINT OF VIEW
 = grams of gold in the bracelet
 = grams of copper in the bracelet
18K gold is supposed to be 75% gold (25% something else) by weight,
and in an alloy, the volumes of the metals mixed add up to the volume of the mix.
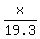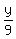 = cubic centimeters of gold in the bracelet
 = cubic centimeters of copper in the bracelet
 -->
My system of equations (with the way I defined x and y) is
To solve by substitution, I solve for ,
--->  ,
and then substitute that expression for in ,
 (rounded)
so  .
The percent copper is 
CONCLUSION:
Since 18K gold is supposed to be 75% gold (25% something else) by weight, the bracelet has more gold than 18K gold.
|
|
|
