Question 919179: Two sides an angle of a triangle are given, determine whether the given measurements produce one triangle, two triangles or no triangle at all.
a = 10 b = 9 A = 30 degrees
(Im very stuck on this problem and the choices they give us is like B = what or C = and also C1 and B1 etc.
please help!
thank you
Found 3 solutions by DrBeeee, MathTherapy, KMST:
Answer by DrBeeee(684)   (Show Source): (Show Source):
You can put this solution on YOUR website! I don't know how to draw on line, so bear with me!
Draw a horizontal line 10 units long and label it AC, this is your line a.
Use your protractor to draw a line 30 degrees above and about point A. This is angle A = 30. Now measure 9 units along that 30 degree line and label the end point as B. This line AB is your line b = 9. Now draw a line to join point B and point C on line AC. This line is c. Got the triangle? Hope so.
Now you need to do some trig to find B, C and c.
To do this, drop a line from point B down to and perpendicular to line AC. Label the point of intersection M, and label the line as h. Now you have a right triangle ABM, where AB = 9 and A = 30 degrees. Label the line AM as x. then we have
(1) cos(A) = x/9 or
(2) x = 9*cos(A) or
(3) x = 9*cos(30) or
In the same triangle we have
(4) sin(A) = h/9 or
(5) h = 9*sin(30) or
(6) h = 4.5 (this is exact because sin(30) = 1/2)
So far so good.
Look at your triangle and label the line MC as y. Note that
(7) x + y = a = 10 or
(8) y = 10 - x or
(9) y = 10 - 9*cos(30)
Also note that
(10) tan(C) = h/y or
(11) tan(C) = 4.5/(10 - 9*cos(30)) or
(12) C = arctan(4.5/(10 - 9*cos(30)))
Use your calculator to find
(13) angle C is approx 63.887... degrees.
Using the identity
(14) A+B+C = 180 we have
(15) 30 + B + 63.887... = 180 or
(16) angle B is approx 86.113... degrees.
Lastly we need c. We can use
(17) sin(C) = h/c or
(18) c = 4.5/sin(C)
Using your calculator and C of (12) we get
(19) line c is approx 5.0115
We can check c using
(20) c^2 = y^2 + h^2 or
Is (5.0115^2 = 2.20577^2 + 4.5^2)?
Is (5.0115^2 = 4.8654... + 20.25)?
Is (5.0115^2 = 25.1154...)?
Is (5.0115^2 = 5.0115^2)? Yes
Answer: The given values form a single scalene triangle ABC, whose sides are a=10, b=9 and c=5.0115... with anles A = 30, B = 86.113... and C = 63.887... degrees.
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two sides an angle of a triangle are given, determine whether the given measurements produce one triangle, two triangles or no triangle at all.
a = 10 b = 9 A = 30 degrees
Use the law of sines to determine how many possible triangles there are


10 sin B = 9 sin 30 -------- Cross-multiplying

 ≈ ≈ 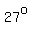
Therefore, angles are: A:  , B: , B: 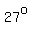 , and C: , and C: 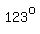 (180 – 30 - 27, or 180 - 57) (180 – 30 - 27, or 180 - 57)
Now, since sin ∠B is: 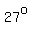 , another possible measure of ∠B is its reference angle: , another possible measure of ∠B is its reference angle: 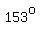 , in the 2nd quadrant. , in the 2nd quadrant.
However, ∠B CANNOT possibly be 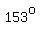 since that would result in ∠B ( since that would result in ∠B (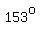 ) + ∠A ( ) + ∠A ( ) being equal to ) being equal to 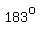 , ,
which is >  . .
Thus, ONLY ONE (1) triangle can be formed with the given measurements
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Having the measures of one angle and the opposite side, you can use law of sines to try to solve the triangle.
In this case, you can use A, a and b to find B, C and c).
Law of sines says that  , so , so
 --> --> --> --> --> -->
That means that  (rounded). (rounded).
That is the only possible measure for  for the only possible triangle with the given measurements. for the only possible triangle with the given measurements.
 too, too,
but you could not have angles measuring  and and 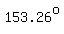 in the same triangle, in the same triangle,
because  . .
So there is only one option, one triangle,
just one  and one and one  , no , no 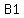 or or 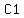 . .
 --> --> --> --> --> --> (rounded). (rounded).
Law of sines also says  <--> <--> , so , so
 --> --> (rounded)--> (rounded)--> (rounded)--> (rounded)--> (rounded). (rounded).
When you draw the  angle, you can locate angle, you can locate
point A, at the vertex of the angle,
ray AB on one side of the angle,
and point C, at distance  from A on the other side of the angle (side AC). from A on the other side of the angle (side AC).
You know that point B is at distance  from point C, from point C,
and that it is on ray AB,
so you just draw an arc with radius  centered at point C. centered at point C.
The point where that arc intersects ray AB is point B.
angle
|
|
|