SOLUTION: In a polygon , two of the external angles are 55 degree and 35 degree and others are equal , each equal to 27 degree . Find the number of sides of the polygon

Algebra ->  Polygons -> SOLUTION: In a polygon , two of the external angles are 55 degree and 35 degree and others are equal , each equal to 27 degree . Find the number of sides of the polygon       Log On


   

Question 917766: In a polygon , two of the external angles are 55 degree and 35 degree and others are equal , each equal to 27 degree . Find the number of sides of the polygon
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The external angles are the angles you have to turn at each corner as you go around the polygon.

Naturally, after you complete one turn around the polygon, you are facing the same way as when you started, so you have turned a total angle of 360%5Eo .
The sum of the measures of all those external angles is 360%5Eo .
Your teacher (or the book) had to tell you that, but isn't it obvious now that I put it that way?

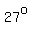Let's say n= number of angles measuring 27%5Eo . Then,
55%5Eo%2B35%5E0%2Bn%2A27%5Eo=360%5Eo--->90%5E0%2Bn%2A27%5Eo=360%5Eo--->n%2A27%5Eo=360%5Eo-90%5Eo--->n%2A27%5Eo=270%5Eo--->n=270%5Eo%2F27%5Eo--->n=10 .
That tells you that the polygon had the two external angles measuring 55%5Eo and 35%5Eo ,
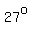plus 10 angles measuring 27%5Eo each,
for a total of 2%2B10=12 external angles.
A polygon with 12 external angles must have 12 internal angles and highlight%2812%29 sides.

NOTE:
I like to assume that the polygon is a convex polygon, so you are always turning in the same direction (always veering right, or always turning to your left).
Otherwise, you would have to measure turns in one direction as positive angles, and turns in the other direction as negative angles. Then, adding angles gets complicated.