Question 917246: Please explain how I would determine the middle point on this graph and end behavior of the rational function:
f(x) = (8x-4x^2)/((x+2)^2)
What I know so far from this rational function is:
Vertical asymptote: x = -2
Horizontal asymptote: y = -4
X-intercept: (2,0),(0,0)
Y-intercept: (0,0)
Here is the graph in it's entirety: http://i.imgur.com/RIr1udF.png
What I want to know is how can I w/o a calculator figure out the middle point on the graph, I have (0,0) and (2,0) and understand that fine but how do I find that middle one freehand?
How do I know when the curve at the 3rd quadrant will appear? I don't understand why that is there.
Please explain as much as possible.
Thanks!
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! "Middle point" would be the local maximum, which on inspecting the graph appears to be x=1/2, and y=1/2.
 , factored, your function.
If you want to exactly find that "middle point" on the graph, that local maximum, you can use first derivative, and equate to zero. This should be easy IF you have enough derivative Calculus skill; otherwise, you will learn this in first semester of Calculus.
You want to know about the end-behavior. Notice the degree of numerator and denominator both 2. The ratio of the leading terms will directly give you the horizontal asymptote, which is the end-behavior. You already found this asymptote pre-assumed to be done correctly. You would have compared  to  ; unbounded in either direction, the other terms in the rational expression become increasingly LESS significant, and the end behavior (a limit) approaches 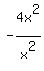 which simplifies to  .
Quadrant 3 Question:
Just test the signs of the intervals that are part of x<0. If f is negative, then that is in quadrant 3.
|
|
|
