Question 916261: One cage contains 2 white mice and 3 black ones, and another cage contains 4 white mice and 3 black ones. A cage is chosen at random and three mice are selected. Find the expected number of white mice in the sample.
I keep getting the wrong answer for this problem, I thought you did the number of ways to choose three mice (0-3) and find their probabilities and then continue to find the mean and that was the answer?
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! Cage1: 5mice, 2W, 3B , p(w) = 2/5)
Cage2: 7mice: 4W, 3B, p(w) = 4/7
cage1 0r cage2 is chosen at random and three mice are selected, n = 3
expected number of white mice
W
0 P(x =0) = 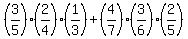 Choosing cage1 0r cage2 Choosing cage1 0r cage2
1 P(x=1) = 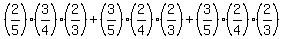 + +
2 P(x=2) = binompdf( 5, .4, 2) + binompdf(7, 4/7, 2) = similar to the above
3 P(x=3) = binompdf( 5, .4, 3) + binompdf(7, 4/7, 3) =
expected = 0•P(x =0) + 1•P(x =1) + 2•P(x =2) + 3•P(x =3)
|
|
|