SOLUTION: If a triangle has a side that is 7 in and the second side that is 2 inches less than twice the third side. What are the possible lengths of the second and third sides?

Look at any triangle.  For instance,  



The shortest distance between two points is the straight
line connecting them.  Therefore here are the requirements 
for a triangle:

1. It is a shorter distance to go from A to B by going straight
from A to B along side AB than it is to go from A to B by
going first to C along side AC and then going from C to B
along side BC.  Therefore AB < AC+BC

2. It is a shorter distance to go from A to C by going straight
from A to C along side AC than it is to go from A to C by
going first to B along side AB and then going from B to C
along side BC.  Therefore AC < AB+BC

3. It is a shorter distance to go from B to C by going straight
from B to C along side BC than it is to go from B to C by
going first to A along side AB and then going from A to C
along side AC.  Therefore BC < AB+AC 

And therefore the sum of any two sides of a triangle must be greater 
than the other side. Now let's look at your problem:

Let the third side be x, then the second side is 2x-2

The sides are then: 

First side = 7 
Second side = 2x-2
Third side = x

1. First side + Second side > Third side

 x < 7+(2x-2)
 x < 7+2x-2
 x < 5+2x 
-x < 5
 x > -5

2. First side + Third side > Second side

 2x-2 < 7+x 
    x < 9


3. Second side + Third side > First side

 7 < 2x+2+x
 7 < 3x+2
 5 < 3x
  < x

So if  < x < 9, all three requirements are true.

Or you can change the improper fraction to a mixed number:

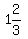 < x < 9
Edwin