|
Question 9147: I need help on finding the number of different starting teams if five basketball players are chosen from a team of ten players
Answer by DWL(56)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a permutation and combination problem. I'll Give you the answer, but you need to read about these two subjects.
Permutation Part
Now we have 10 players and want to make groupings of 5 people. It's harder to list all those permutations. To find the number of five-people permutations that we can make from 10 people without repeated (10_P_5), we'd like to have a formula because there are 30,240 such permutations and we don't want to write them all out!
For five-people permutations, there are 10 possibilities for the first person, 9 for the second, 8 for the third, and 7 for the fourth, and 6 for the last person. We can find the total number of different five-people permutations by multiplying 10 x 9 x 8 x 7 x 6 = 30,240. This is part of a factorial
To arrive at 10 x 9 x 8 x 7 x 6, we need to divide 10 factorial (10 because there are ten objects) by (10-5) factorial (subtracting from the total number of objects from which we're choosing the number of objects in each permutation). You can see below that we can divide the numerator by 5 x 4 x 3 x 2 x 1:
10_P_5 = 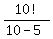 = = 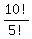 = = 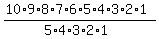 = = 
Combination Part
we have 10 people from which we wish to choose 5 and we want to find the number of combinations of size 5 without repeated people that can be made from the ten people. To calculate 10_C_5, which is 120, we don't want to have to write all the combinations out!
Since we already know that 10_P_5 = 30,240, we can use this information to find 10_C_5. Let's think about how we got that answer of 30240. We found all the possible combinations of 5 that can be taken from 10 (10_C_5). Then we found all the ways that five people in those groups of size 5 can be arranged: 5 x 4 x 3 x 2 x 1 = 5! = 120. Thus the total number of permutations of size 5 taken from a set of size 10 is equal to 5! times the total number of combinations of size 5 taken from a set of size 10: 10_P_5 = 5! x 10_C_5.
When we divide both sides of this equation by 5! we see that the total number of combinations of size 5 taken from a set of size 10 is equal to the number of permutations of size 5 taken from a set of size 10 divided by 5!. This makes it possible to write a formula for finding 10_C_5:
10_C_5 = 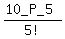 = = 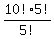 = = 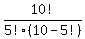 = = 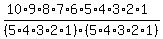 = = 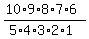 = = 
So the answer is:
You can have 252 starting teams of five from a group of 10 players.
|
|
|
| |