Question 914387: A man has $210,000 invested in three properties. One earns 12%, one 10% and one 8%. His annual income from the properties is $20,200 and the amount invested at 8% is twice that invested at 12%.
(a) How much is invested in each property?
12%=
10%=
08%=
(b) What is the annual income from each property?
12%=
10%=
08%=
I can get the first equation out of the first sentence because its easy.

but the second one just confuses me. This is the equation that i got from the sentence
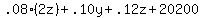
I don't know if its wrong and I can't figure out what to do after it.
Answer by JoelSchwartz(130)   (Show Source): (Show Source):
You can put this solution on YOUR website! x=amount invested at eight percent
y=amount invested at twelve percent
z=amount invested at ten percent
x=2y
x+y+z=210,000
3y+z=210,000
z=210,000-3y
.08x+.12y+.1z=20,200
.08x+.12y+.1(210,000-3y)=20,200
.08x+.12y+21,000-.3y=20,200
.16y+.12y-.3y=-800
-.02y=-800
y=40,000
z=210,000-120,000
z=90,000
x=80,000
.08*80,000=6,400 annual income for eight percent
.1*90,000=9,000 annual income for ten percent
.12*40,000=4,800 annual income for twelve percent
|
|
|