|
Question 913984: Please help me solve this problem:
A circle of radius 1 is centered at the origin and passes through the point (1/2,3√/2).
(a) Find an equation for the line through the origin and the point (1/2,3√/2).
y=
(b) Find an equation for the tangent line to the circle at (1/2,3√/2).
y=
[Hint: A tangent line is perpendicular to the radius at the point of tangency.]
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A circle of radius and centered at the origin and passes through the point 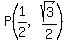 . .
The equation for a line that starts with that starts with "y =" is the equation in slope-intercept form,
 , where , where  is the slope and is the slope and  is the y-intercept. is the y-intercept.
(a) The line through the origin,  , and the point , and the point 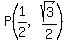
has a y-intercept of  , and , and
a slope of 
The equation for the line hrough the origin and the point 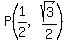 that starts with "y =" is that starts with "y =" is
 . .
(b) The tangent line to the circle at the point 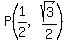 goes through the point of tangency, goes through the point of tangency, 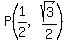 . .
The radius of the circle at the point of tangency is the line segment that connects the points  and and 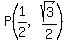 . .
That line segment is part of the line with equation  and slope and slope  found in part a). found in part a).
According to the hint, the tangent you are looking for is perpendicular to that line and passes through the point of tangency, 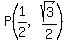 . .
The line perpendicular to a line with slope  , has a slope of , has a slope of 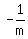 . .
So, for the tangent you are looking for,
the slope is  . .
That is more elegantly expressed as

The equation of that tangent in point-slope form, based on point 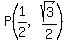 is is
 . .
If you wanted to express that equation in slope intercept form, you would "distribute" and "solve for y", like this:
 ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> --->
|
|
|
| |