Question 913117: I'm not sure where to begin on this. I'm in Algebra II, but I feel like this is more of a pre-calc question. Any ideas? United Parcel Service has contracted you to design a closed box with a square base that
has a volume of 10,000 cubic inches. Initially they would like to know the dimensions of such a
box with minimum surface area. They are considering creating the box with a reinforced bottom.
The box would be made out of a cardboard material costing 1cent per square inch to build the walls
and top, however the bottom would be constructed with stronger material, costing 2cents per square
inch to build. How do the dimensions of the box having the minimum surface area compare to the
dimensions of the reinforced box which costs the least?
Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website! The beginning for both of the functions first attends volume.
Bottom is a square shape, so if x is the sidelength for the bottom (as well as top), and if y is height of box, then
and from it,  .
TOTAL SURFACE AREA
Let A be variable for total surface area, to be formed into a function of x.
 which you might possibly want as a single numerator expression and a single denominator expression.
COST FUNCTION
1 cent per sq in. for walls and top; 2 cents per sq. in. for bottom.
Let C be the cost for the box.
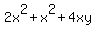
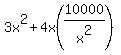
The form of the area function and the cost function are the same. Both are rational functions. They show the same format.
The question to minimize and then compare the dimensions of these two functions seems outside of and beyond Algebra II; but might be used in College Algebra, but more likely fit in Calculus 1. Very likely most Algebra II students are allowed, encourage, even TAUGHT TO USE a graphing calculator, so if this is something you know how to use, you can find useful results. Decide on the x value or pick what seems to correspond to each minimum, and use the value to evaluate y.
...
AREA
COST
|
|
|
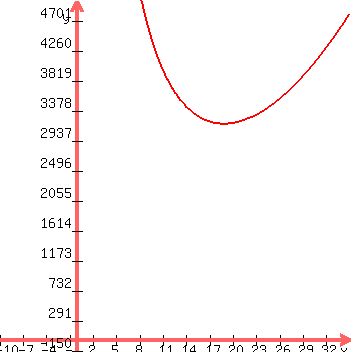
