|
Question 912785: Howdy, having a little problem with this question, not sure if it's supposed to be a piecewise function or what.
The question goes:
The graph of f is concave down for 0<=x<=6. Which is bigger, (f(3)-f(1))/(3-1) or (f(5)-f(3))/(5-3)? Why?
Not exactly sure how you'd go about solving this; Most of the book before this has given a formula or a table to use, this question does not.
Pardon if this is in the wrong section, it looks like a function and I'm not quite certain if I'm supposed to be solving it, or graphing, or what.
Found 2 solutions by josgarithmetic, jim_thompson5910:
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! My impulse is to say, we need to know what kind of graph and maybe what is the x at the maximum. A possibility could be that f(3)>f(1) and then 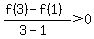 ; and that f(5)<(f(3) and then  . This could mean that the first ratio is GREATER than the second ratio.
That can all be wrong if the graph or the actual function make for the discussion I gave to be wrong.
Answer by jim_thompson5910(35256) (Show Source):
You can put this solution on YOUR website! This function's interval of [0,6] has been split up into these two intervals: [1,3] and [3,5]
It turns out that the slopes of the secant lines will be decreasing in a concave down section of a graph. It's somewhat connected to the idea that the tangent line slopes are decreasing.
Since the interval [1,3] is to the left of [3,5], this means (f(3)-f(1))/(3-1) will be larger. Both slopes are negative, but (f(3)-f(1))/(3-1) is closer to 0, therefore larger.
-------------------------------------------------------
Imagine the flip scenario: say (f(5)-f(3))/(5-3) is larger. This would mean that the slopes are increasing, but this would mean you're on a concave up section of the graph. So this contradicts what we're given.
Hopefully it's making sense.
Let me know if you need more help or if you need me to explain a step in more detail.
Feel free to email me at jim_thompson5910@hotmail.com
or you can visit my website here: http://www.freewebs.com/jimthompson5910/home.html
Thanks,
Jim
|
|
|
| |
