SOLUTION: Help with the x-intercept and vertical asymptote of rational functions {{{(4x^2+72x+320)/(x^2+9x-10)}}} VA = I have no idea HA = 4? x-int = no idea y-int = 0,-32 ==

Algebra ->  Functions -> SOLUTION: Help with the x-intercept and vertical asymptote of rational functions {{{(4x^2+72x+320)/(x^2+9x-10)}}} VA = I have no idea HA = 4? x-int = no idea y-int = 0,-32 ==      Log On


   

Question 911752: Help with the x-intercept and vertical asymptote of rational functions

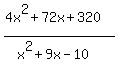
%284x%5E2%2B72x%2B320%29%2F%28x%5E2%2B9x-10%29
VA = I have no idea
HA = 4?
x-int = no idea
y-int = 0,-32
======================
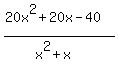
%2820x%5E2%2B20x-40%29%2F%28x%5E2%2Bx%29
VA = no idea
HA = 20?
x-int = no idea
y-int = 0,-40
======================
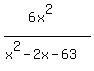
%286x%5E2%29%2F%28x%5E2-2x-63%29
VA = -7,9
HA = 6
x-int = no idea
y-int = 0,-63

Please make any corrections and help with the missing ones.
Thank you in advance.
Found 2 solutions by josgarithmetic, ichigo449:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Notice that each example uses numerators and denominators of degree 2. This is an indication, the degree of numerator and denominator equal, of the rational expression having a horizontal asymptote.

Doing ONLY your first example:

%284x%5E2%2B72x%2B320%29%2F%28x%5E2%2B9x-10%29

%284%28x%5E2%2B18x%2B80%29%29%2F%28%28x%2B10%29%28x-1%29%29

%284%28x%2B8%29%28x%2B10%29%29%2F%28%28x-1%29%28x%2B10%29%29

Vertical Asymptote at x=1, because function will there be undefined.

Removed Point at x=-10, a hole in the graph, because you have a factor of 1=(x+10)/(x+10) which is undefined for x=-10.

x-intercept is VERY OBVIOUSLY at x=-8. The function will be equal to 0 for x=-8.

You were unsure about horizontal asymptote, but what value you reported makes sense. You could try multiplying numerator AND denominator by 1%2Fx%5E2 and ponder how each term behaves as x tends to the right or to the left without bound. The leading terms will make the rational expression approach 4, as you reported; since the nonleading terms approach zero, and you have something resembling 4%2F1.

Answer by ichigo449(30) About Me  (Show Source):
You can put this solution on YOUR website!
Rather than doing the question I will give you general info on rational functions as you seem confused:
A rational function is a function that can be written as the ratio of two polynomials where the denominator isn't zero.
f(x) = p(x) / q(x)
Domain
The domain of a rational function is all real values except where the denominator, q(x) = 0.
Y-Intercepts
Thinking geometrically, y-intercepts will occur when x = 0 so finding them becomes a simple f(0) = p(0)/q(0).
Roots
The roots, zeros, solutions, x-intercepts (whatever you want to call them) of the rational function will be the places where p(x) = 0. That is, completely ignore the denominator. Whatever makes the numerator zero will be the roots of the rational function, since 0/anything = 0.
If you can write it in factored form, then you can tell whether it will cross or touch the x-axis at each x-intercept by whether the multiplicity on the factor is odd or even.
Vertical Asymptotes
An asymptote is a line that the curve approaches but does not cross. The equations of the vertical asymptotes can be found by finding the roots of q(x). Completely ignore the numerator when looking for vertical asymptotes, only the denominator matters.
If you can write it in factored form, then you can tell whether the graph will be asymptotic in the same direction or in different directions by whether the multiplicity is even or odd.
Asymptotic in the same direction means that the curve will go up or down on both the left and right sides of the vertical asymptote. Asymptotic in different directions means that the one side of the curve will go down and the other side of the curve will go up at the vertical asymptote.
Horizontal Asymptotes
A horizontal line is an asymptote only to the far left and the far right of the graph. "Far" left or "far" right is defined as anything past the vertical asymptotes or x-intercepts. Horizontal asymptotes are not asymptotic in the middle. It is okay to cross a horizontal asymptote in the middle.
The location of the horizontal asymptote is determined by looking at the degrees of the numerator (n) and denominator (m).
If n If n=m, then y=an / bm is the horizontal asymptote. That is, the ratio of the leading coefficients.
If n>m, there is no horizontal asymptote. However, if n=m+1, there is an oblique or slant asymptote.
Using this information you can hopefully do the question. Good luck.