Question 911344: At noon a train leaves cleveland and heads due north at 10 mph. Another train leaves at 1pm going due east at 20 mph. how fast is the distance between them changing at 3pm?
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! Hey wait, trains don't leave north out of Cleveland, they'd end up in Lake Erie.
But anyways.
Find the distance between them,
At 1pm, the first train is already 10 miles north and it's distance is,
 , where t starts counting at 1pm.
The second train's distance is,
 eastbound.
The two distances form the legs of a right triangle.
To calculate the distance between them find the hypotenuse.
To find the rate of change of D, take the derivative with respect to  .
So at 3pm, 
So then,
 
|
|
|
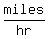
