Question 910574: Do I have this correct?
consider the rational function:
x-intercept: numerator set to zero, therefore (-12,0)
y-intercept: all x's set to zero, therefore (0,12)
Vertical Asymptote: set denominator to zero to find restraints, therefore -2,2 would it be both?
Horizontal Asymptote: compare degrees 12x^0/x^2 so y=0 or none.
Do I have this correct? please describe what I have correct or incorrect in my reasoning.
Thank you
Found 2 solutions by Edwin McCravy, AnlytcPhil:
Answer by Edwin McCravy(20064)   (Show Source):
You can put this solution on YOUR website! Do I have this correct?
consider the rational function:
x-intercept: numerator set to zero, therefore (-12,0)
No, the numerator is 12. You cannot set 12 equal to 0.
12 is always 12, never 0. So there is no x-intercept.
The graph does not intersect the x-axis.
y-intercept: all x's set to zero, therefore (0,12)
No. To set x=0 means to replace x by 0.
Vertical Asymptote: set denominator to zero to find restraints, therefore -2,2 would it be both?
No,
Take square roots of both sides:
It's the 0 that ± not the 2. When 0 is ±, it's just at x=0.
Horizontal Asymptote: compare degrees 12x^0/x^2 so y=0 or  .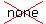
No y=0 MEANS the x-axis is the horizontal asymptote, not "none".
Here is the graph, gotten by plotting and connecting points
(-8,.12),(-6,.1875), (-4,.333), (-3,.48), (-2,.75), (-1,1.333), (0,3), (1,12),
(3,12), (4,3), (5, 1.333), (6,.75), (7,.48), (8,.333), (10,.1875), (12,.12)
Notice that it does not cross the x-axis, has y-intercept (0,3),
has green vertical asymptote at x=2, and horizontal asymptote which
is the x-axis, whose equation is y=0.
Edwin
Answer by AnlytcPhil(1808)  (Show Source):
You can put this solution on YOUR website! Question 910574
Do I have this correct?
consider the rational function:
x-intercept: numerator set to zero, therefore (-12,0)
No, the numerator is 12. You cannot set 12 equal to 0.
12 is always 12, never 0. So there is no x-intercept.
The graph does not intersect the x-axis.
y-intercept: all x's set to zero, therefore (0,12)
No. To set x=0 means to replace x by 0.
Vertical Asymptote: set denominator to zero to find restraints, therefore -2,2 would it be both?
No,
Take square roots of both sides:
It's the 0 that ± not the 2. When 0 is ±, it's just at x=0.
Horizontal Asymptote: compare degrees 12x^0/x^2 so y=0 or .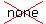
No y=0 MEANS the x-axis is the horizontal asymptote, not "none".
Here is the graph, gotten by plotting and connecting points
(-8,.12),(-6,.1875), (-4,.333), (-3,.48), (-2,.75), (-1,1.333), (0,3), (1,12),
(3,12), (4,3), (5, 1.333), (6,.75), (7,.48), (8,.333), (10,.1875), (12,.12)
Notice that it does not cross the x-axis, has y-intercept (0,3),
has green vertical asymptote at x=2, and horizontal asymptote which
is the x-axis, whose equation is y=0.
Edwin
|
|
|
