What we are to prove is that for any positive integer n,
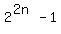 is divisible by 3, that is, it is a multiple of 3.
For n=1
is divisible by 3, that is, it is a multiple of 3.
For n=1
 . 3 is a multiple of 3.
So it's true for n=1
We must prove that if you know it's true for integer n=k,
then it will be true for n=k+1.
Assume it's true for n=k.
. 3 is a multiple of 3.
So it's true for n=1
We must prove that if you know it's true for integer n=k,
then it will be true for n=k+1.
Assume it's true for n=k.
 for some positive integer m
Multiply both sides by
for some positive integer m
Multiply both sides by 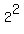
 for some positive integer m
for some positive integer m
 for some positive integer m
for some positive integer m
 Write -4 as -1-3
Write -4 as -1-3


 is a
multiple of 3.
Therefore since the theorem is true for n=k=1, it's true for n=k+1=2.
And since the theorem is true for n=k=2, it's true for n=k+1=3
Thus since the theorem is true for n=k=3, it's true for n=k+1=4
And this goes on forever, for we've proved it can't stop!
Edwin
is a
multiple of 3.
Therefore since the theorem is true for n=k=1, it's true for n=k+1=2.
And since the theorem is true for n=k=2, it's true for n=k+1=3
Thus since the theorem is true for n=k=3, it's true for n=k+1=4
And this goes on forever, for we've proved it can't stop!
Edwin