|
Question 90952: I posted this word problem and received an answer - but I am still confused about how to solve it - sorry
Problem:
Your company needs to make both long and short range missiles. Production cannot make more than 50 missiles and no more than 30 long range types. Your company spends $60,000 to make a short range missile and $90,000 to make a long range missile and has no more than 3.6 million to spend. Find the maximum profit your company can make if they receive $400,000 for each short range misssile and $850,000 for each long range missile. how many long range missiles can they make???
I still am so confused about this and don't know the complete answer
I need the following:
constraints
objective function
graph and SOLUTION!!!!!!! PLEASE HELP!!!THANKS
llo
Answer by kev82(151)   (Show Source):
You can put this solution on YOUR website! Hi,
This is a linear programming problem. What exactly don't you understand? Are you having trouble with LP problems in general or just this one?
I don't just want to go through and give you all the working because I don't know where you're having trouble, and you haven't really shown any working. However, I'll try and point you in the right direction and we'll see what happens.
You will often see the words objectives and constraints when solving these problems, and it's quite important to know what they mean.
Constraints are inequalities (or very rarely equations) that limit your variables. For example you can't make -3 of something, and you only have 10.5 hours to do something are constraints. They constrain the variables.
Objectives are an equation (or equations if you do really advanced stuff - some of my work is in multi objective LP) that you are trying to maximize or minimize.
A lot of LP problems are about making stuff, and luckily so is this one. Normally it is a good choice to set your variables to the amount of each item you want to make, but beware this isn't always the case. The objective is normally profit, and you want to maximize it
So here we're making two types of missiles, a long range and short range one. Let's let  be the number of long range missiles we make, and  be the number of short range missiles we make.
Now, reading through the problem, let's look for constraints. The first thing resembling a constraint says that the production department can make at most 50 missiles. The number of missiles is just the number of long range plus the number of short range, so we can write that as  . The next constraint says we can make at most 30 long range ones, so  .
The next constraint is a bit more compliacted, it says we can only spend 3600000 dollars, and we know that each long range missile costs 90000 and each short range costs 60000. If we built 3 long range missiles, that would cost us 3*90000=270000 right? Well, similarly if we built long range missiles then it will cost us 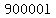 . Can you see how the constraint is  ? You can divide by 30000 if you like, makes it a bit easier to draw.
There are two more constraints left, that I gave a hint for above, can you figure out what they are? As another hint they are not listed in the problem, they are just common sense!(you need to figure out what the other two are to solve the problem.
Now, on to the objective. The question says you want to maximise profit, well what is profit? it's the amount of money you make after costs. A long range missile costs you 90000, and you sell it for 850000, so you make 760000 profit per long range missile, similarly you make 340000 per short range missile (check you agree with 340000). This means your profit for selling long range, and short range is 
Now, if you draw all the constraints on a graph (there are lessons on here for drawing inequalities) then you will end up with a closed region, also known as the feasable region. This is where all the constraints are satisfied. You can pick any point in this region and it will satisfy the constraints.
The rule of LP says that the maximum value if the objective function, is at a vertex (a point where the inequalities cross) You can do some fancy math to figure out which vertex it is, but in a case like this where there are only 5 constraints, it is probably easier to try all the vertices.
See if you agree with all my constraints and see if you can figure out the other two. Then try to draw them all on a graph. After that figure out the vertices and see which one has your maximum profit.
Good luck.
Kev
|
|
|
| |
