Question 909476: I need someone who is good in physics i need help please .i do not understand this question.
An athlete executing a long jump leaves the ground at 28.0 angle and travels 7.80 m a)What was the take off speed? b)If this speed were increased by just 5.0%,how much longer would the jump be?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The athlete left the ground with an initial velocity of magnitude  (in m/s), making an angle of (in m/s), making an angle of  with the ground. The magnitude and direction of the athlete's velocity changed over time under the influence of the acceleration of gravity, with the ground. The magnitude and direction of the athlete's velocity changed over time under the influence of the acceleration of gravity,   downwards, until the athlete landed on the ground , downwards, until the athlete landed on the ground ,  seconds after leaving the ground. seconds after leaving the ground.
The velocity can be decomposed into a horizontal component of magnitude 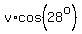 , ,
and a vertical component of magnitude 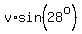 . .
FOR THE HORIZONTAL COMPONENT OF THE MOTION:
We assume that the athlete is jumping over a perfectly horizontal surface, and that air resistance does not really affect him/her at the speeds he/she is capable of attaining.
That makes his horizontal speed constant at 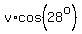 for the for the  seconds the athlete is airborne. seconds the athlete is airborne.
As a consequence of our assumptions, we know that
the athlete's initial horizontal velocity (in m/s)
times the time in the air ( , in seconds) , in seconds)
equals the horizontal displacement,  in meters (7.8 m, in this case). in meters (7.8 m, in this case).
So, in general  , ,
and in this particular case  . .
FOR THE VERTICAL COMPONENT OF THE MOTION:
The vertical component of the velocity changes from 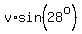 to zero over to zero over 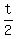 seconds, at a constant rate of seconds, at a constant rate of   . .
So,  ---> ---> ---> ---> ---> --->
PUTTING IT ALL TOGETHER:
How are  and and  related? related?
Putting together  and and  we get we get
 ---> --->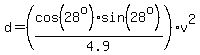
Substituting the approximate values  and and  , ,
to get the approximate formula 
WHAT DOES THAT TELL YOU?:
a) At this point you can use  to calculate to calculate  : :
 ---> ---> ---> ---> ---> ---> --> --> (rounded). (rounded).
So, the initial velocity was  m/s. m/s.
b) If an athlete jumps at the same angle, with  times the initial velocity, he/she will get times the initial velocity, he/she will get  times as far. times as far.
If the athlete jumps with 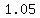 times (5% more) initial velocity, times (5% more) initial velocity,
he/she will get  times farther. times farther.
That would be  (rounded). (rounded).
So, jumping with 5% higher initial velocity, the athlete will travel 8.7 meters.
That means that his/her jump would be
8.6 m - 7.8 m =  m longer, m longer,
or 1.10 times longer (10% longer).
|
|
|