Question 909255: write an equation for a quadratic given the following:
x-intercepts are (2,0) and (5,0) and y-intercept is (0,6)
I know that it means I have (x-2) and (x-5) for my equation. I multiplied them to get x^2 - 7x + 35. I'm not sure how to incorporate the y-intercept.
Do I put the equation equal to 6 and solve?
6= x^2 - 7x + 35
Is my answer x^2 - 7x -29?
Found 3 solutions by Alan3354, Edwin McCravy, AnlytcPhil:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! write an equation for a quadratic given the following:
x-intercepts are (2,0) and (5,0) and y-intercept is (0,6)
I know that it means I have (x-2) and (x-5) for my equation. I multiplied them to get x^2 - 7x + 35. I'm not sure how to incorporate the y-intercept.
Do I put the equation equal to 6 and solve?
6= x^2 - 7x + 35
Is my answer x^2 - 7x -29?
At the y-intercept, x = 0
For x^2 - 7x -29, at x = 0, y = -29
--> No, that's not it.
---------------
x^2 - 7x + 10 is correct for the x-intercepts. (not 35)
You have to "adjust" it to get the y-int of (0,6).
Adding 6 shifts it upward, and affects the x-intercepts, too.
---
Multiply it by a constant to make the 10 --> 6
--> 6/10 or 3/5
==============
(3/5)*(x^2 - 7x + 10) = 3x^2/5 - 21x/5 + 6
3x^2/5 - 21x/5 + 6 = 0
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
The other tutor gave you a way that will work ONLY if you are given
the intercepts. But you should do it a more general way, because
the three points you are given will not always be intercepts. For
instance you may be given the points (7,6), (-3,24) and (12,42).
Here's what you should do instead. You must start with
y = ax˛ + bx + c
Then you substitute in each of the three points, the x-coordinate
for x, and the y-coordinate for y.
Substituting (2,0)
y = ax˛ + bx + c
0 = a(2)˛ + b(2) + c
0 = 4a + 2b + c
Substituting (5,0)
y = ax˛ + bx + c
0 = a(5)˛ + b(5) + c
0 = 25a + 5b + c
Substituting (0,6)
y = ax˛ + bx + c
6 = a(0)˛ + b(0) + c
6 = 0 + 0 + c
6 = c
Now you have three equations:
0 = 4a + 2b + c
0 = 25a + 5b + c
6 = c
Substitute 6 for c in the first two:
0 = 4a + 2b + 6
0 = 25a + 5b + 6
Eliminate the b's by multiplying the first equation by -5
and the second equation by 2
0 = -20a - 10b - 30
0 = 50a + 10b + 12
-------------------
0 = 30a - 18
18 = 30a
 = a
 = a
Substitute for a in
0 = 25a + 5b + 6
0 = 25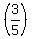 + 5b + 6
0 = 15 + 5b + 6
0 = 21 + 5b
-21 = 5b
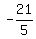 = b
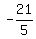Now substitute for a, = b, and 6 for c in
y = ax˛ + bx + c
and get:
This method will always work whether the points given happen to be
intercepts or not.
Edwin
Answer by AnlytcPhil(1806)  (Show Source):
You can put this solution on YOUR website! Question 909255
The other tutor gave you a way that will work ONLY if you are given
the intercepts. But you should do it a more general way, because
the three points you are given will not always be intercepts. For
instance you may be given the points (7,6), (-3,24) and (12,42).
Here's what you should do instead. You must start with
y = ax˛ + bx + c
Then you substitute in each of the three points, the x-coordinate
for x, and the y-coordinate for y.
Substituting (2,0)
y = ax˛ + bx + c
0 = a(2)˛ + b(2) + c
0 = 4a + 2b + c
Substituting (5,0)
y = ax˛ + bx + c
0 = a(5)˛ + b(5) + c
0 = 25a + 5b + c
Substituting (0,6)
y = ax˛ + bx + c
6 = a(0)˛ + b(0) + c
6 = 0 + 0 + c
6 = c
Now you have three equations:
0 = 4a + 2b + c
0 = 25a + 5b + c
6 = c
Substitute 6 for c in the first two:
0 = 4a + 2b + 6
0 = 25a + 5b + 6
Eliminate the b's by multiplying the first equation by -5
and the second equation by 2
0 = -20a - 10b - 30
0 = 50a + 10b + 12
-------------------
0 = 30a - 18
18 = 30a
= a
= a
Substitute for a in
0 = 25a + 5b + 6
0 = 25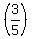 + 5b + 6
0 = 15 + 5b + 6
0 = 21 + 5b
-21 = 5b
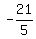= b
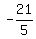Now substitute for a, = b, and 6 for c in
y = ax˛ + bx + c
and get:
This method will always work whether the points given happen to be
intercepts or not.
Edwin
|
|
|
